개요
스탠포드대 강의인 cs276 information retrieval의 강의를 공부한뒤 강의 슬라이드를 정리하는 포스팅이다. 어디까지나 자의적인 이해와 해석이 있는만큼 참고할 분들은 비판적 사고로 접근하기를 권장한다.
이번 강의에서는 Dictionary & Tolerant Retrieval에 대해 소개한다.
This lecture
- Dictionary data structures
- “Tolerant” retrieval
- Wild-card queries
- Spelling correction
- Soundex
Dictionary data structures for inverted indexes
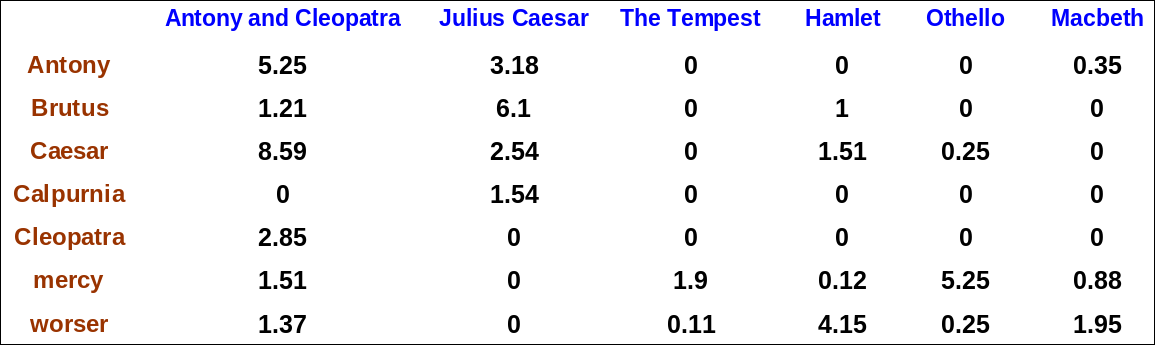
Dictionary 데이터 구조는 단어와, 문서내의 빈도와 포스팅 리스트이 빈도를 어떻게 관리하는가?
아래는 standaard inverted index이다.
Dictionary data structures
주로 선택은 아래의 2가지로 IR 시스템 마다 다르다.
- 해시 테이블
- 트리구조
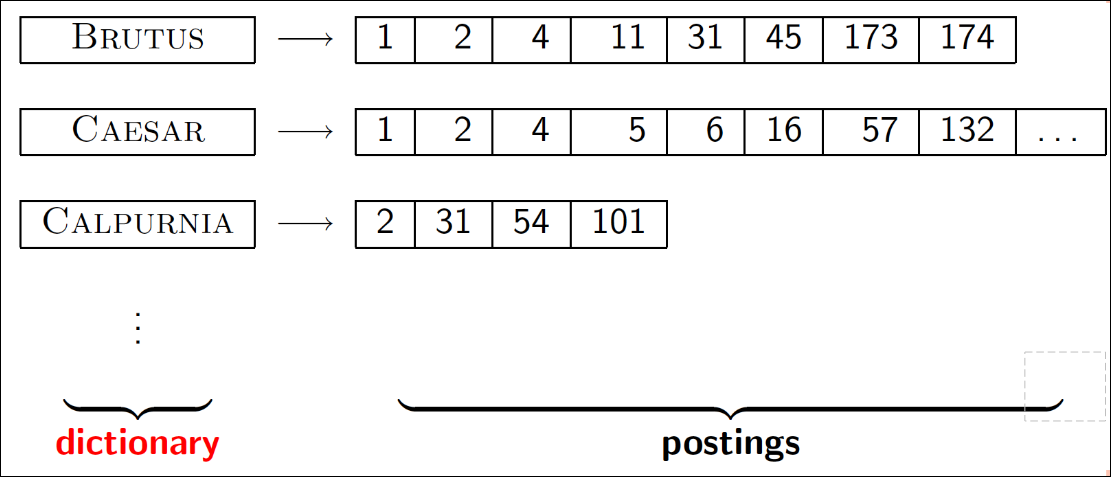
Hashtables
- 각 단어를 정수값으로 해시함
- 장점
- 트리보다 lookup이 빠름: $O(1)$
- 단점
- 작은 변형을 검색하기 쉽지 않음
- judgment/judgement
- prefix 검색이 안됨
- 만약 단어가 계속 증가한다면 주기적으로 전체 데이터를 re-hash 해야할 수 있음 (예를 들어 해시 함수가 10만개까지 커버할수 있었다면 잘못하면 100001번째는 다시 1번째 해시값으로 충돌할 여지가 있기 때문)
Trees
가장 심플한 것은 이진 트리이다. 아래와 같이 알파벳 정렬에 의한 이진트리를 구성할 수 있다.
단점은 예를 들어 1, 2, 3, 4, 5, 6 순서로 값이 입력되면 트리가 오른쪽으로만 계속 증가해서 직선이 되어 버린다.
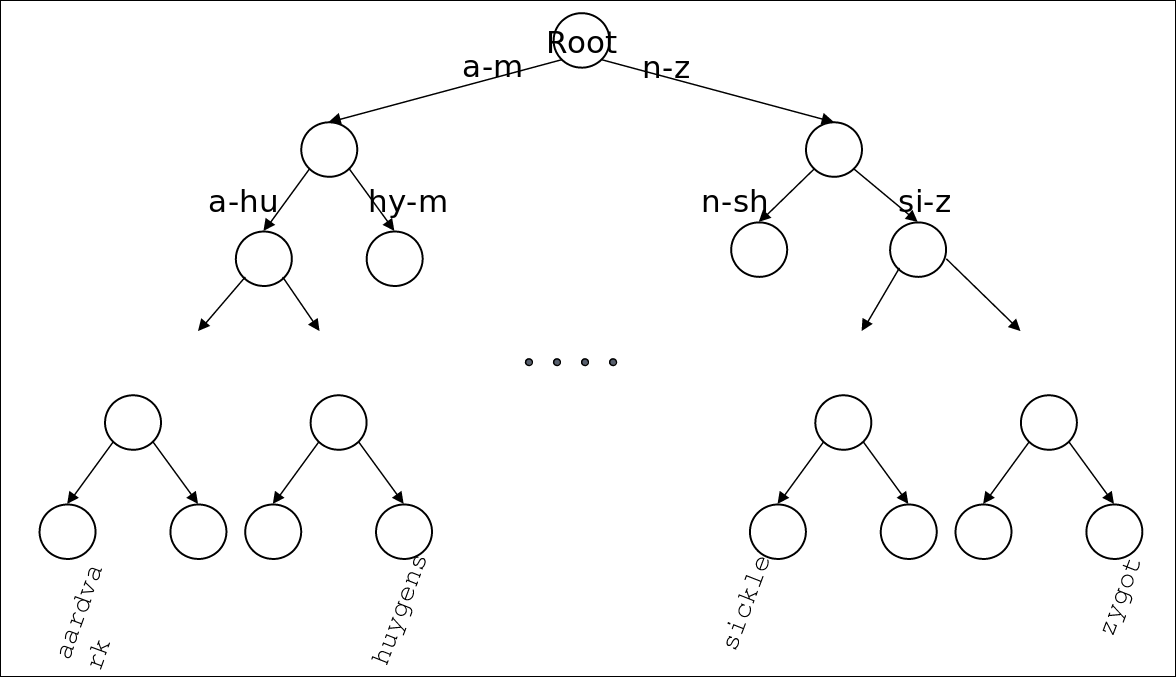
따라서 가장 일반적인것은 B-트리 이다.
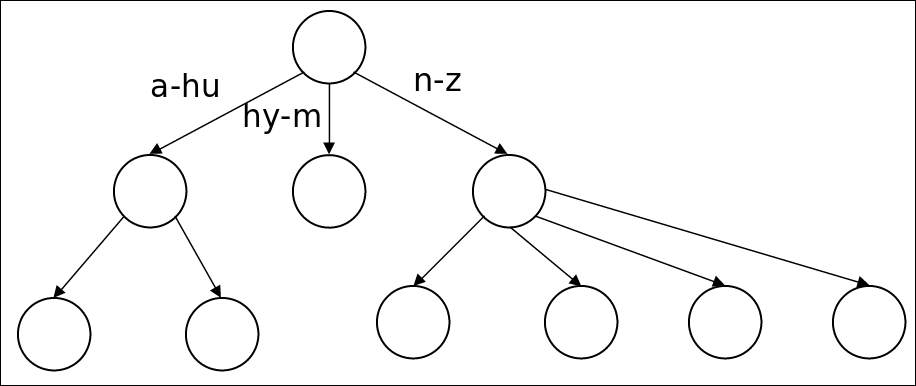
- 장점
- prefix 문제를 해결 할 수 있다. (“예를 들어 “app”로 시작하는 apple, application을 모두 찾을 수 있다.)
- 단점
- 느리다: $O(logM)$, 따라서 balanced tree가 필요할 수 있음
- 이진 트리를 rebalance하는게 비용이 비싸다. (하지만 B-트리는 rebalance문제를 완화시킨다.)
Wild-card queries: *
- mon*: mon으로 시작하는 모든 문서를 찾는다.
- 이진트리(또는 B-트리)에서는 해결이 쉬움 $ mon \le w \le moo $, (n다음이 o니까 이를 이용)
- “*mon”을 찾는건 더 어렵다.
- 단어를 뒤집은 추가적인 B-tree를 운영하는게 방법
B-trees handle *’s at the end of a query term
- 중간에 위치하는 와일드 카드는 어떻게 처리할 수 있을까?
- co*tion
- 떠오르는 방법은 B-트리에서 co*와 *tion 사이를 조회하여 둘의 교집합을 구한다.
- 비용이 비싸다.
- 해결책: 와일드 카드 쿼리를 변형하여 단어의 끝에 위치하게 바꿈.
- 이것이 루씬에서의 Permuterm 인덱스이다.
Permuterm index
중간에 위치하는 와일드 카드를 해결하기 위한 방법이다. 예를 들어 “hello”라는 단어가 있다고 가정해보자. Permuterm Index는 한국어로 바꾸어 보면 순열 인덱스이다. 순열이라는 단어가 들어가 있듯이 우선 색인 요청이 들어오기전 아래와 같이 단어를 순서대로 만든다.
여기서 중요한 것은 특수문자 $로써 term의 끝을 알린다. 제일 앞에 위치하면 앞에 더이상 글자가 없다는 뜻이고 반대로 제일 뒤에 위치하면 뒤에 더이상 글자가 없다는 뜻이다.
| Permuterm |
|---|
| hello$ |
| ello$h |
| llo$he |
| lo$hel |
| o$hell |
| $hello |
쿼리 예제는 아래와 같다.
| 쿼리 | lookup 대상 |
|---|---|
| X | X$ |
| X* | $X* |
| *X | X$* |
| * X *(실제론 space가 없다.) | X* |
| X*Y | Y$X* |
permuterm 계산 알고리즘은 $표시를 하고 쿼리를 *패턴이 항상 뒤로 오도록 permutation하면 된다. 말로하면 어려운데 예를 들어 *X이라면 X뒤에 아무것도 더 존재하지 달러표시를 붙여주고 그다음 *이 제일 뒤로 오게끔 permutation한다.
| Permuterm 계산 순서 |
|---|
| *X |
| *X$ |
| X$* |
퀴즈 : hel별o를 찾는 방법은? X별Y 문제가 되므로 X=hel, Y=o로 볼 수 있다. 따라서 Y달러X별을 looup하면 되므로 o달러hel별을 찾으면 된다.
Spell Correction
- 주요한 아이디어
- 색인 타이밍에 correction을 고려
- 검색 타이밍에 correction을 고려
- 두가지 취향
- isolated word
- 각 단어의 스펠링을 체크함
- 단어가 제대로된 스펠링이라면 교정되지 못함 (예: from -> form, 빨리 타이핑 하다보면 늘 틀린다.)
- context sensitive
- 주변의 단어를 살펴봄 (예: I flew form Heathrow to Narita.)
Document correction
- 특별히 OCR된 문서에 필요함
- domain specific 단어
- OCR에서는 O와 D가 자주 헷갈리고 키보드 타이핑에서는 O와 I가 키가 붙어있어 오타일 확률이 높다.
- 하지만 웹 페이지나 프린트 된 자료도 오타가 있음
- 목표는 사전이 오타를 거의 포함하지 않는 것이다.
- 하지만 종종 문서를 수정하는 것 대신 쿼리-문서 맵핑을 고친다.
Query mis-spellings
- 이 부분에 집중한다
- 둘중에 하나에 해당
- 정확한 문법의 문서를 획득
- 몇몇 제안된 대체 쿼리를 리턴함
Isolated word correction
- 근본적인 전제는 올바른 문법의 사전이 있음
- 2가지 옵션
- 기본 사전
- 영어사전
- 산업에 특화된 단어들
- 색인된 말뭉치 사전
- 웹의 모든 단어
- 모든 고유명사
Isolated word correction
- 주어진 사전과 문자열 순서 Q가 있다면 Q에 가까운 사전의 단어를 리턴함
- 가깝다는 정의는?
- 우리가 살펴볼 것
- Edit Distance(Levenshtein distance)
- Weighted Edit Distance
- n-gram 오버랩
Edit Distance
- 문자열 $S_1$, $S_2$가 있다면 서로 같아지게 변환시킬 수 있는 최소한의 숫자
- 문자열 단위의 연산
- Insert, Delete, Replace
- 예를들어 아래와 같은 비용이 든다.
- dof -> dog : 1
- cat -> act : 2
- cat -> dog : 3
- 일반적으로 dynamic programming으로 검색함
Weighted Edit Distance
- 위의 로직에서 일부 문자열에 가중치를 적용함
- OCR 또는 키보드 에러
- o와 i는 상대적으로 적은 거리차이가 나게끔 가중치를 조정함
- 이부분은 확률 모델을 적용 할 수 있음
- 가중치 행렬을 input으로 사용함
- 가중치를 handle하기 위해 dynamic programming을 수정함
Using edit distances
- Given query, first enumerate all character sequences within a preset (weighted) edit distance (e.g., 2)
- Intersect this set with list of “correct” words
- Show terms you found to user as suggestions
- Alternatively,
- We can look up all possible corrections in our inverted index and return all docs … slow
- We can run with a single most likely correction
- The alternatives disempower the user, but save a round of interaction with the user
Edit distance to all dictionary terms?
Edit Distance 방법으로 스펠 체크를 할 때 모든 사전 단어 사전에 대해 Edit Distance를 구해야 하나?
- 주어진 오타가 포함된 쿼리와 사전의 모든 단어의 편집거리를 비교하는 것은 비용이 비싸다.
- 대안으로 단어의 후보군의 커트라인을 정할 수 없나?
- 가능성 있는 하나는 n-gram overlap이다.
- 이것 자체가 spelling correction으로 쓰일 수 있다.
N-GRAM OVERLAP
N-GRAM OVERLAP은 아래의 일을 수행한다.
- 쿼리 스트링의 모든 n-gram을 순회한다.
- n-gram 색인을 통해 사전의 단어에서 매치되는 n-gram이 있는지 찾아본다.
- 매치 되는 n-gram의 threshold를 둔다.
Example with trigrams
Trigram으로 예제를 한번 살펴보자.
- 쿼리 : december
- nov, ove, vem, emb, mbe, ber
- 사전의 단어 : december
- dec, ece, cem, emb, mbe, ber
3개의 trigram이 overlap 된것을 확인 할 수 있다. 오버랩 된 숫자가 쿼리와 단어의 유사도를 의미한다.
그렇다면 위 방식을 좀 더 noramlize할 수 있을까?
One option – Jaccard coefficient
- n-gram overlap을 측정하는 일반적인 방법이다.
- X와 Y의 유사도를 보기 위해 아래와 같이 계산한다. $ | X \cap Y| / | X \cup Y | $
- 계수 1은 같은 단어를 의미하고 0은 서로 연관성이 없음을 얘기한다.
- X와 Y의 크기가 같을 필요는 없다.
- 항상 0~1사이의 값이므로 thrashold를 따로 정할 수 있다.
Bigram index + Jaccard
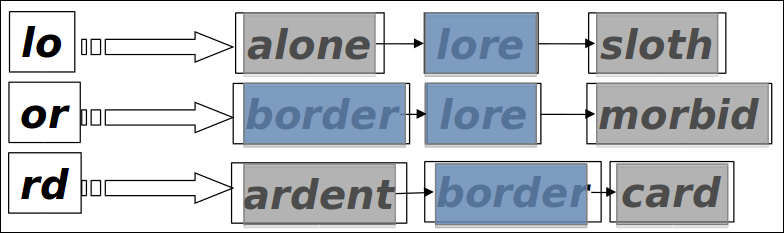
예를 들어 lord랑 비슷한 3개의 bigram중에 2개가 매치되는 단어를 찾아본다고 해보자. 그러면 아래와 같이 이를 만족하는 단어는 lore, border를 구할 수 있다.
Context Sensitive Spell Correction
문맥을 고려한 spell 교정은 아래와 같은 문장이 있으면 단어는 오타가 없지만 문맥상 오류가 있는 form을 from으로 고치고 싶은 것이다.
I flew form Heathrow to Narita.
요즘의 똑똑한 검색 엔진이 “I flew from Heathrow to Narita.을 의미하나요?” 이렇게 제안을 해주는 기능으로 활용된다.
Probabilistic Language Models
문장에 확률을 할당하는 것으로 아래와 같이 활용 될 수 있다.
- Machine Translation
- P(high winds tonite) > P(large winds tonite)
- Spell Correction
- P(about fifteen minutes from) > P(about fifteen minuets from)
- Speech Recogniton
- P(I saw a van) >> P(eyes awe of an)
Probabilistic Language Modeling
실제로 모델링을 한다면 문장의 확률을 계산하거나 단어의 순서를 계산하는 것이다.
모델은 $ P(W) or P(W_n|W_1,W_2,…,W_{-1})$를 계산한다.
계산하는 방법은 P(its, water, is, so, transparent, that)와 같이 chain rule을 계산하는 것이다.
여기서의 chain rule은 아래와 같은 확률의 연쇄법칙을 의미한다.
$ P(A,B,C,D) = P(A)P(B|A)P(C|A,B)P(D|A,B,C)$
일반화 된 수식으로 나타내면 아래와 같다.
$ P(x_1,x_2,x_3,…,x_n) = P(x_1)P(x_2|x_1)P(x_3|x_1,x_2)…P(x_n|x_1,…,x_{n-1})$
확률에 대한 기본 개념은 따로 정리해돈 머신러닝에 필요한 확률 정리를 참고하자.
How to compute P(W)
즉 위의 규칙을 통해 예문을 계산한다면 아래와 같다.
P(“its water is so transparent”) = P(its) × P(water|its) × P(is|its water) × P(so|its water is) × P(transparent|its water is so)
Markov Assumption
하지만 위의 방법은 구체적으로 동일한 문장이 무수히 많아야 제대로 동작할 것이다. 따라서 Markov가 이 가정을 단순화 했다. 아래의 2개중 하나로 가정한다.
P(the | its water is so transparent that ) $\simeq$ P(the| that)
P(the | its water is so transparent that ) $\simeq$ P(the| transparent that)
Approximating Shakespeare

Soundex
- 쿼리를 음성이 같은 것으로 분류하는 것
- 언어에 종속적이다
- 예: chebyshev -> tchebycheff
Soundex – typical algorithm
- 모든 토큰을 4글자의 reduced form으로 표현한다.
- 쿼리 term에도 동일하게 적용
- reduced form으로 색인과 검색을 수행함
- 단어의 첫번째 문자를 얻음
- 다음의 문자가 일어난 것을 0으로 바꿈 A, E, I, O, U, h, W, Y
- 다음의 레터를 아래와 같이 바꿈 B, F, P, V -> 1 C, G, J, K, Q, S, X, Z -> 2 D,T -> 3 L -> 4 M, N -> 5 R -> 6
- 연속된 숫자의 쌍을 모두 제거함
- 결과 문자열의 모든 0을 제거함
- 결과 문자열을 <대문자>, <숫자>, <숫자>, <숫자>로 변환함
예를 들어 Herman -> H655 이다.
- H를 얻는다.
- 다음 모음을 0으로 만든다. 그러면 H를 제외하고 나머지 문자가 0rm0n 이 남을 것이다.
- 레터 변환을 한다. 06505가 된다.
- 연속된 숫자는 제거한다.
- 결과에서 0을 제거한다. 6555가 된다.
- 결과 문제열을 정리하면 h6555가 된다.
Hermann도 4번 과정을 통해 같은 코드를 얻게 된다.
Soundex
- Soundex는 고전적 알고리즘으로 대부분의 DB에서 제공한다.
- 정보검색에서는 그닥 유용하지는 않다.
- “high recall” 작업에서 쓸만한데 예를 들어 인터폴에서 용의자 정보를 음성만을 통해 찾을때 유용하게 쓸 수 있다. 이를테면 살인사건 용의자 이름이 스미스라는 정황이 있는데 이 사람 철자가 Smith인지 Cmith인지 확실치 않을때 유용하게 쓸 수 있고 이는 precision을 높이지는 못하지만 실제 recall을 높이는 효과가 있다.
- 기본 알고리즘이 라틴기반 언어 기준이라 한계점이 있다.
Index Construction
Distributed indexing
- 웹 스케일의 색인은 반드시 분산 환경이어야함
- 개별 장비는 장애대비가 되어 있어야함
MapReduce
- 색인을 생성하는 알고리즘은 MR의 인스턴스이다.
- 색인 생성은 하나의 단계이다.
- 다른 단계: term으로 분할된 색인을 문 서로 분할된 색인으로 변환하는 것
- term-partitioned : 하나의 장비가 term들을 다룸
- document-partitioned : 하나의 장비가 document들을 다룸
- 대부분의 검색엔진은 문서-분할 기반의 색인으로 load balancing에 더 유리하다.
Schema for index construction in MapReduce
간단한 MR의 함수 schema는 아래와 같다.
- map : input -> list(k, v)
- reduce : (k, list(v)) -> output
색인 과정에서의 MR은 아래와 같은 동작이다.
- map
- input
- colleciton
- output
- list(termId, docId)
- reduce
- input
- (termId1, list(docId)), (termId2, list(docId)), …)
- output
- (posting list1, posting list2, …)
Example for index construction
색인 예제를 한번 다뤄보자.
- map
- input
- d1 : C came, C c’ed
- d2 : C died
- output
- <C, d1>, <came, d1>, <C, d1> <C’ed, d1>, <C, d2>, <died, d2>
- reduce
- input
- (<C,(d1,d2,d1)>, <died,(d2)>, <came,(d1)>, <c’ed,(d1)>)
- output
- (<C,(d1:2,d2:1)>, <died,(d2:1)>, <came,(d1:1)>, <c’ed,(d1:1)>)
Dynamic Indexing
- 현재까지는 컬렉션이 정적이라고 가정했다.
- 새로운 케이스는:
- 문서가 시간마다 들어오고 insert될 필요가 있음
- 문서가 수정되거나 삭제됨
- 기존과 달리 사전과 포스팅 리스트는 수정되어야함:
- 포스팅은 사전에 포함된 term마다 수정되어야 함
- 새로운 term은 사전에 추가되어야함
Dynamic indexing at search engines
- 대부분의 검색 엔진은 동적 색인을 지원함
- 그들의 인덱스는 증분의 변화를 가짐
- 새로운 상품
- 새로운 블로그
- 새로운 웹 페이지
- 하지만 주기적으로 index를 새로 만듦
- 쿼리 processing이 old index 에서 new index로 바뀌고 old index를 삭제함
Index Compression
TODAY
아래의 압축에 대해 배워보자.
- Dictionary compression
- Postrings compression
Why compression (in general)?
- 디스크 용량을 적게 차지
- 비용 효율
- 메모리를 더 활용 할 수 있음
- 캐시에 올릴수 있는 양이 늘어나기 때문
- 속도 증가
- 디스크에서 메모리로 올리는 시간이 감소됨
- 압축된 데이터를 메모리로 올리는 속도와 메모리에 올라온 데이터를 해제하는 속도가 빨리짐
- 가정: 압축해제 알고리즘이 충분히 빠르다
- 우리가 사용하는 알고리즘에 있어 가정을 사실로 만들수 있음
Why compression for inverted index?
- 사전
- 메인 메모리에 적재할만큼 충분히 작게 만듦
- 몇몇 포스팅 리스트도 메인 메모리에 올릴만큼 충분히 작게 만듦
- 포스팅 파일
- 디스크 공간 절약이 필요함
- 디스크로 부터 읽는 포스팅 리스트를 읽는 시간을 줄여야 함
- 대형 검색 엔진은 상당한 양의 포스팅 리스트를 메모리에 보관함
- 압축은 메모리에 더 많이 보관 가능케함
- 다양한 IR에 특화된 압축 scheme을 고안함
Lossless vs. lossy compression
- 무손실 압축
- 모든 정보가 보존됨.
- 대부분의 IR에서 사용
- 손실 압축
- 일부 정보를 폐기함
- 일부의 전처리 과정은 손실 압축임
- case folding
- stop words
- stemming
- number elimination
- 차후 다룰 내용은 어떠한 top k 쿼리에도 포함되 지 않을것 같은 포스팅 리스트는 잘라냄
- top k 리스트 입장에서는 거의 손실이 없음
Compression
- 이제 사전과 포스팅에 대한 압축을 고려해보자.
- 오직 basic boolean index에서만
- positional index에 대한 연구가 없음
- compresison scheme에 대해 고려해볼 예정
Why compress the dictionary?
- 검색은 사전과 함께 시작함 -> 이 사전을 메모리에 올려놓고 싶음
- 메모리 적재는 다른 어플리케이션과 경쟁을 요한다.
- 모바일 디바이스는 메모리가 상대적으로 적음
- 만약 사전이 메모리에 없더라도 사전 용량이 작아 검색 startup time을 적게 만들고 싶음
- 따라서, 사전에 대한 압축은 중요하다.
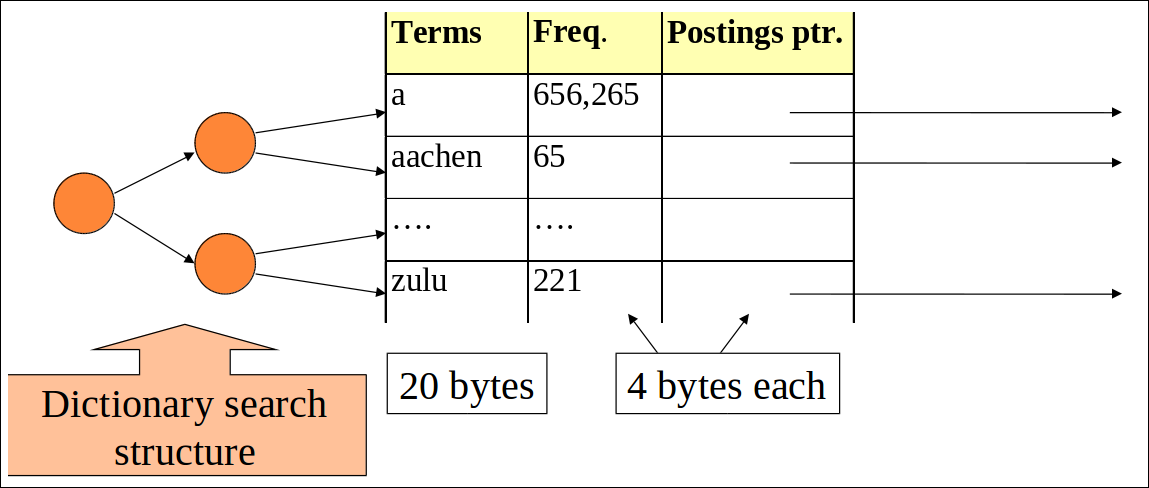
Dictionary storage – first cut
- fixed-width 엔트리
- 약 40만 term을 관리하는데 term당 28바이트면 약 11.2MB가 소모됨
Fixed-width terms are wasteful
- 대부분의 term의 byte가 낭비됨
- 영어서적의 경우 단어당 평균 4.5글자를 차지함
- 왜 사전의 크기를 예측하기 위해 이 숫자를 사용하지 않을까?
- 영어사전의 평균 글자수는 8글자임
- 왜 이 수치 또한 활용하지 않을까?
- 짧은 단어가 토큰 갯수를 압도하지만 type average가 압도하지는 않는다.
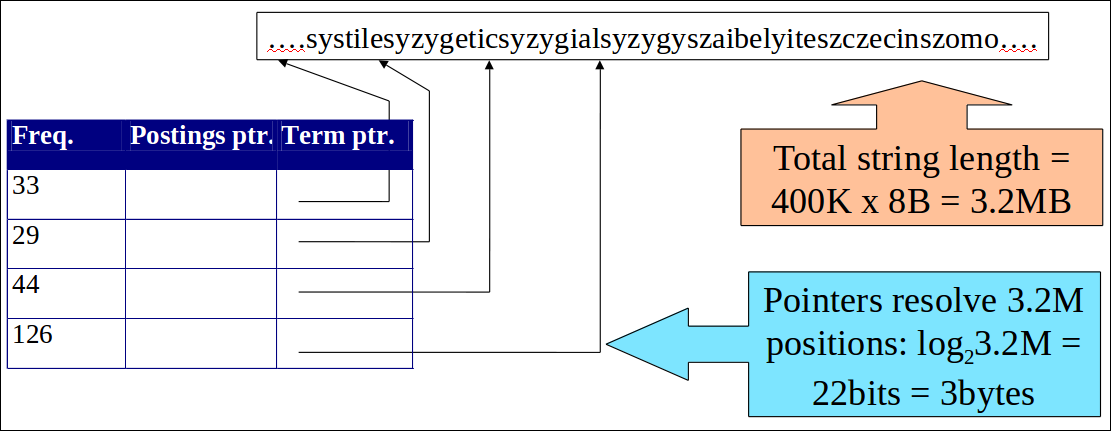
Compressing the term list: Dictionary-as-a-String
- 사전을 엄청나게 긴 문자열로 저장
- 다음 단어에 대한 포인터가 현재 단어의 끝을 의미
- 사전 공간의 약 60%를 절약함
Space for dictionary as a string
- 4 바이트 : term frequency
- 4 바이트 : term당 포스팅에 대한 포인터
- 3 바이트 : term 포인터
- 평균 8 바이트 : term당 term string
- 400K terms x 19 = 7.6 MB (고정 길이 일때 11.2MB 대비 이득)
Blocking
- 매 k번째 term 문자열마다 포인터를 저장함.
- 예: k=4
- Need to store term lengths (1 extra byte)
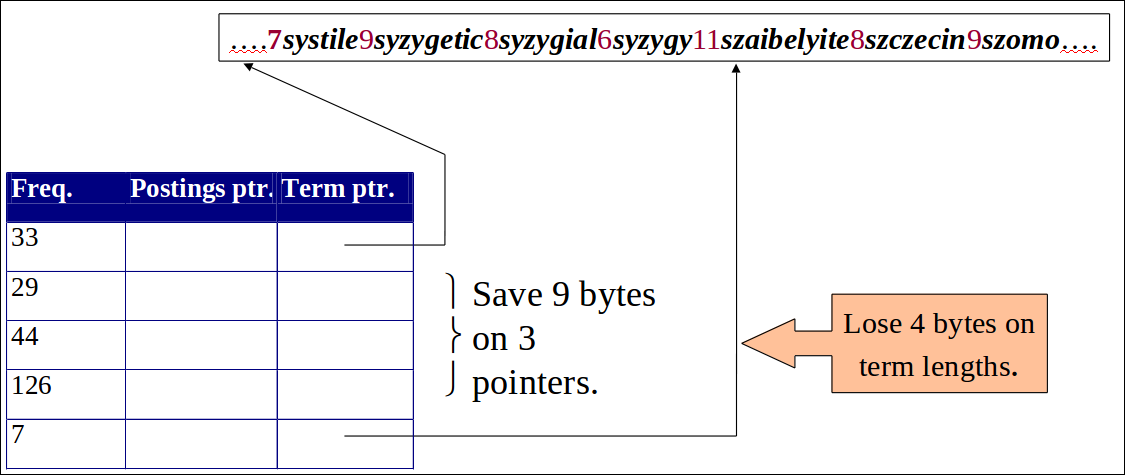
NET
- 블럭 사이즈가 k = 4라고 가정
- 포인터당 3바이트를 Blocking 없이 사용한다면
- 3 * 4 = 12 바이트
- 이제 우리는 3 + 4 = 7 바이트를 사용함
또다른 0.5MB를 절약하는 것이다. 이것은 사전 크기를 7.6MB -> 7.1MB로 만든다. k값이 크면 절약의 폭이 더 크다.
Postings file entry
- term을 포함하는 문서를 docId가 증가하는 순서로 저장함.
- computer: 33, 47, 154, 159, 202, …
- 개선: 첫 docId만 제대로 기입하고 그다음 docId 부터 값의 차이를 저장
- computer: 33, 14, 107, 5, 43, …
- 최초는 33, 그다음부터 (47-33), (154-47), …
- 긍정적인점 : 대부분의 값차이는 20비트 미만의 공간을 차지함
Three postings entries
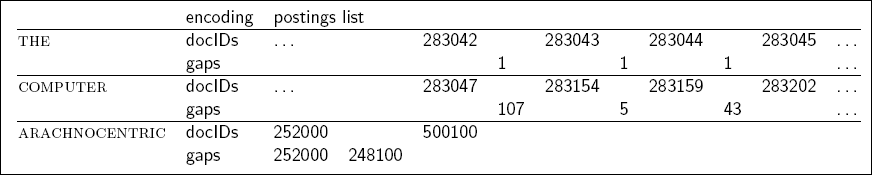
Variable length encoding
- 목표:
- arachnocentric단어에 우리는 gap당 20비트 미만의 엔트리만 사용한다.
- for단어에 우리는 1비트의 gap만 사용한다.
- 만약 term의 평균 gap이 G라면 우리는 $log_2G$ bits/gap을 사용하길 원한다.
- 핵심 Cahllenge:
- gap으로 표시하는 모든 정수를 더 적은 비트로 인코딩하는것.
- 이것은 variable length encoding을 필요로 한다.
- 가변 길이 인코딩은 더 작은 숫자들로 인코딩함으로써 구현한다.
Variable Byte (VB) codes
- gap G에 있어 $log_2G$를 만족할만한 가정 적은 바이트를 사용하고 싶음
- 만약 $ G \le 127$이면 바이너리 인코딩 인코딩에서 7개 비트를 사용하고 c를 1로 잡는것이다.
- 아니면 G의 낮은 순서의 7비트는 인코딩하고 추가 바이트는 높은 순위의 비트를 같은 알고리즘으로 인코딩하는 것이다.
- 끝을 의미할때는 마지막 바이트를 1(c=1)로 표시하고 아닐때는 0으로 표시한다.
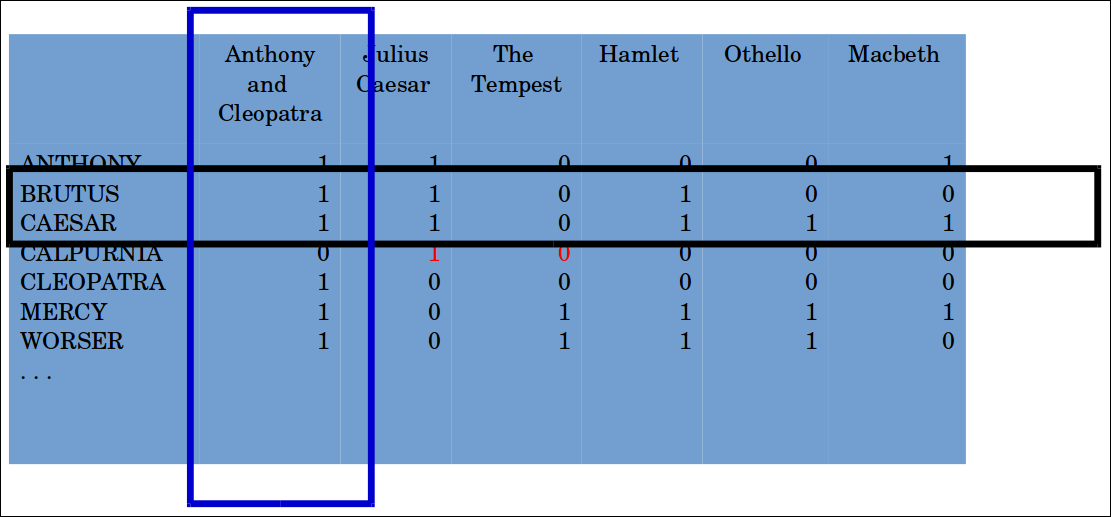
Vectorizing Text— Boolean (One-hot)
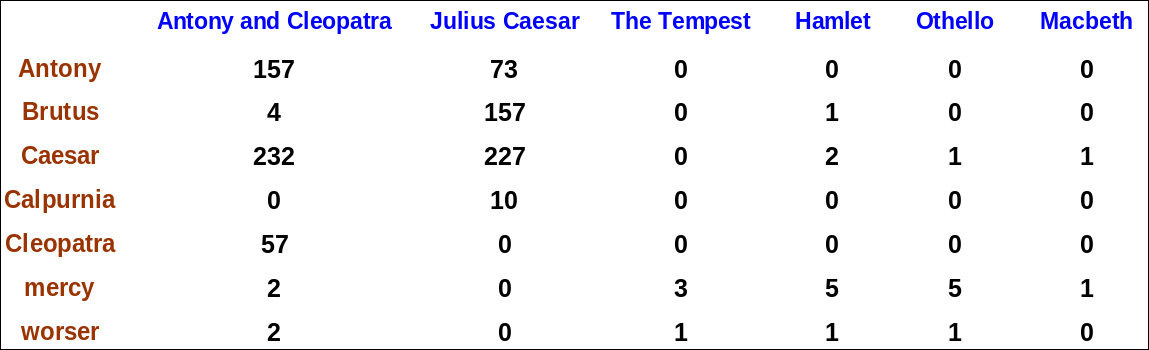
Too many prefect match, Term-frequency (TF)
Boolean → count → tf.idf (sklearn.feature_extraction.text.TfidfVectorizer)