머신러닝에 필요한 확률이론 핵심 정리
개요
머신러닝 공부에 필요한 기본 확률 지식들을 개인적인 용도로 정리하여 포스팅 한다. 하지만 주의할 점은 필자도 완벽히 이해하지 못한 상태에서의 정리라 일부 수식이나 해석이 오류가 있을수 있다. 또한 수식 표현에 있어 가운데 정렬시에만 정상 표현되는 경우가 있어 정렬이 들쑥 날쑥한 점을 양해 부탁 드린다.
왜 확률인가?
- 의사 결정에 있어서 불확실성을 고려하는 것이 매우 중요하다.
- 확률이론은 불확실성을 다루는데 적절한 메카니즘이다.
- 예를들어 사전확률 개념을 알고나면 “대서양에서 고기가 잡혔다면 고기는 배스보다는 연어일 확률이 높다.”의 개념에 대해 이해할 수 있다.
용어 정의
- Random Experiment
사건이 발생하기 전에는 결과를 모르는 실험(예: 주사위 던지기) - Outcome
Random Experiment의 결과 - Sample Space
일어날 가능성있는 outcome들의 집합(예: {1, 2, 3, 4, 5, 6}) - Event
Sample Space의 부분집합(예: 주사위를 던져 홀수가 나오는 experient, {1,3,5})
퀴즈 : 주사위를 2번 던져 앞면이 나올 이벤트를 구하라
정답 : P(H,H), (H,T), (T, H)}
확률의 수식적인 정의
직관적으로 확률의 수식적인 정리를 하면 아래와 같다.
$ N $은 event $ \alpha$가 일어나는 횟수이다.
$ n $은 trial수이다.
$$ P(\alpha) = \lim_{n->\infty } \frac {N(\alpha)}{n} $$
정의를 해석하자면 $ n $을 무수히 많이 시도하면 결국 확률은 수렴한다는 것이다. 예를 들어 주사위에서 특정 숫자가 나올 확률은 $ \frac {1}{6} $이 된다.
확률의 성질
- $ 0 \le P(A) \le 1 $
- $ P(S) = 1 $
-
$ A_1 $ ~ $ A_n $이 서로 독립확률이면 아래 수식을 만족한다.
$$ P(A_1 \cup … \cup A_n) = \sum_{i=1}^n P(A_i)$$ -
$ P(A \cap C) = P(A,C) $
사전 확률(Prior)
충치가 있을 확률 0.1, 충치가 없을 확률 0.9
$ P(Cavity) = 0.1 $
사후 확률(Posterior)
아래의 뜻은 치통이 있는 사람 중에 80%는 충치일 가능성이 있다는 것이다.
$ P(Cavity/Tootache) = 0.8 $
조건부 확률의 수학적 정의는 아래와 같다.
$ P(A|B) = \frac {P(A,B)}{P(B)} $
유사하게 아래와 같이 나타낼 수 있다.
$ P(B|A) = \frac {P(A,B)}{P(A)} $
또한 이를 수식 이동을 통해 아래와 같이 나타낼 수 있다.
연쇄법칙(Chain Rule)이 적용되는 것을 알 수 있다.
$ P(A,B) = P(A|B)P(B) = P(B|A)P(A) $
전체 확률의 법칙(Law of Total Probability)
$ A_1, A_2, …, A_n $이 서로 독립적인 event이고 B는 어떤 이벤트라고 가정한다면 아래와 같은 법칙을 가지게 된다.
의미는 A와 B가 (집합의 개념에서)겹쳐지는 만큼의 조건부확률은 개별 조건부 확률의 합이라는 것이다.
$ P(B) = P(B, A_1) + P(B, A_2) + … + P(B, A_n) $
이 수식은 $ P(A,B) = P(B|A)P(A) $에 의해 아래와 같이 바꿔 나타낼 수 있다.
$ P(B|A_1)P(A_1) + P(B|A_2)P(A_2) + … + P(B|A_n)P(A_n) $
이 수식을 간단하게 나타내면 아래와 같다.
$ \sum_{j=1}^n P(B|A_j)P(A_j) $
베이즈 정리(Bayes Rule)
머신 러닝 관련해서 가장 유명한 수식중 하나를 꼽자면 베이즈 정리가 아닐까 한다.
$ P(A|B) = \frac {P(B|A)P(A)}{P(B)} $
예를 들자면 환자들의 질병과 증상에 대해 얘기해보자. 질병과 증상 확률이 각각 확률일 가질때 주어진 증상에서 특정질병일 확률은 아래와 같이 표현 될 수 있다.
$ P(Disease|Symptom) = \frac {P(Symptom|Disease)P(Disease)}{P(Symptom)} $
이 수식을 이해하는 것이 중요한데 좀더 와닿게 “스팸 필터링” 머신러닝 문제로 이 확률이 어떻게 활용되는지 이해해보자. 스팸메일에서 coupon이란 단어가 들어있을때 스팸메일 확률은 오른쪽의 수식으로 부터 구해질 수 있다. 이때 오른쪽의 수식은 스팸메일 중에 쿠폰이란 단어가 등장할 확률, 전체메일에서 스팸메일일 확률, 스팸 메일에서 쿠폰이란 단어가 등장할 확률로 부터 구해질 수 있다. 재밌게도 이를 이용해 왼쪽의 쿠폰이란 단어가 메일에 포함될 때 스펨메일을 확률을 구할 수 있다.
$ P(spam|coupon) = \frac {P(coupon|spam)P(spam)}{P(coupon)} $
이를 단어 하나가 아니라 메일에서 등장하는 전체단어로 확장하게 되면 Naive Bayes를 이용한 스팸필터 모델이 된다.
스팸메일일 확률 = P(spam|coupon)P(spam|sex)…P(spam|casino)
또하나 예를 들자면 아래와 같은 문제를 생각해보자.
[퀴즈]
뇌수막염을 가진사람의 50%는 목이 뻣뻣하다.
뇌수막염 확률 P(M) 은 5만분의 1이다.
목이 뻣뻣할 확률 P(S) 20분의 1이다.
목이 뻣뻣한 환자가 병원에 오면 이사람의 뇌수막염일 확률은?
그럼 이를 베이즈 정리를 통해 수식화 하면 아래와 같다.
$ P(M|S) = \frac {P(S|M)P(M)}{P(S)} $
$ P(S|M) = 0.5 $
$ P(M) = \frac {1}{50000} $
$ P(S) = \frac {1}{20} $
이를통해 계산하면 $ P(M|S) = 0.0002 $이다.
확률 독립(Independence)
만약 A와 B 사건이 서로 독립이면 아래의 수식을 만족한다.
$ P(A,B) = P(A)P(B) $
뜻은 아래의 조건부 확률 수식에서 서로 독립이면 P(A|B)가 P(A)와 같기 때문이다.
$ P(A,B) = P(A|B)P(B) $
A, B가 C에대해 조건부 독립이면 아래 수식을 만족한다.
$ P(A|B,C) = P(A|C) $
확률변수(Random Variable)
많은 실험에서 원본 확률 구조 보다 요약된 변수가 다루기 쉽다. 이를 위해 Random Variable을 사용한다.
예를 들어 50명이 찬성/반대 설문조사를 했다고 가정해보자.
* 이때 찬성을 1, 반대를 0으로 기록한다.
* 실험에 따른 sample space는 경우의 수에 의해 element수는 $ 2^{50} $이 된다.
element가 너무 많으니 우리는 사실 찬성에 대해서만 관심이 있다고 가정해보자.
* 다시 Random Variable X를 50명중에 1이 기록된 수라고 정의해보자.
* 그러면 0명~50명의 찬성이 있을수 있으니 sample space는 51개의 element를 가진다.
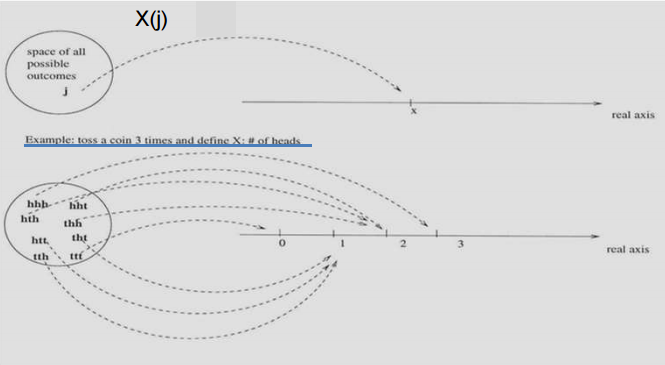
Random Variable은 프로그래밍의 하나의 함수 처럼 Random Experiment의 outcome을 특정 값으로 할당하는 것이다.
예를 들어 Random Variable을 아래와 같이 정의했다고 해보자.
Random Variable = 주사위를 2번 던져 나오는 수의 합
그러면 주사위를 2번 던져 (1,1)이 나왔다면 2로 맵핑된다.
주사위를 예제로 사용한 김에 이를 수식화 하면 아래와 같다.
- $ S = <s_1, s_2, …, s_n> $
- $ X = <x_1, x_2, …, x_n> $
- $X = X_j$를 Random Variable이 관측될때를 뜻한다.
- $s_j \in S $일때 $X(s_j) = x_j$의 의미는 sample space에서 주사위의 합이 $x_j$라는 뜻이다.
이를 수식화해보자.
$$ P(X=x_j) = \sum_{s_j:X(s_j)=x_j}P(S_j)$$
쫄것 없다. 복잡해 보여도 하나하나 보면 이해가 간다.(오히려 SQL 쿼리라고 생각하고 이해해보자.) 예제를 들어보자. 주사위를 2번던져 합이 5가 나올 확률을 위의 수식으로 설명해보자. $P(X=x_j)$의 의미는 random variable이 $x_j$일 확률이란 뜻이다. 이때 $ \sum_{s_j:X(s_j)=x_j}P(S_j)$의 뜻은 sample space는 (1,4), (2,3), (3,2), (4,1)가 나올 확률을 다 더한것이 Random Variable 5가 나올 확률이란 뜻이다.
위 예제를 계산해보면 아래와 같다.
$$ P(X=5)=P((1,4))+P((2,3))+P((3,2))+P((4,1))=4/36=1/9$$
이산/연속 확률 변수(Discrete/Continuous Random Variable)
- 이산 확률변수는 이산값을 가정한다.
- 연속 확률 변수는 연속 확률값을 가전한다.
- Probability mass/density function은 pmf/pdf라고 불린다.
- 대문자 PDF는 Probability Distiribution Function이다.
pmf(probability mass function)
pmf는 이산값의 확률 변수를 표시하기 위한 수단이다.
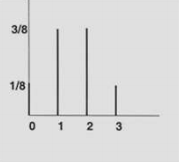
각 $x$의 확률값의 합은 1이기 때문에 아래의 수식으로 나타낼 수 있다.
$$ \sum_x p(x) = 1 $$
a보다 크고 b보다 작은 X의 확률은 아래와 같이 a에서 b사이의 확률의 합으로 나타낼 수 있다.
$$ P(a<X<b) = \sum_{k=a}^b p(k) $$
pdf(probability density function)
pdf는 연속된 확률 변수를 표시하기 위한 수단이다.
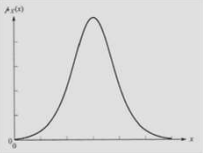
이산값과 달리 연속값이므로 -무한대 ~ 무한대까지 $ p(x) $를 적분하면 전체확률 1이 나온다.
$$ \int_{-\infty}^{\infty} p(x)dx = 1 $$
또한 a ~ b사이의 확률은 아래와 a ~ b 사이의 적분으로 나타낼 수 있다.
$$ P(a < X < b) = \int_{a}^{b} p(t)dt $$
PDF(Probability Distiribution Fuction)
대문자 PDF는 확률이 p(x)이하일때까지의 누적 확률이다.
$ F(x) = P(X \le x) $
PDF는 2개의 성질을 지닌다.
- $ 0 \le F(x) \le 1 $
- $ F(x) $ 는 연속된 함수이다.
만약 이산값을 가지면 PDF는 아래와 같이 나타낼 수 있다.
쉽게 얘기하자면 이산값이면 간단히 sum하고 연속값이면 적분한다.
x가 이산값이면 아래와 같은 수식이 성립한다.
$$ F(x) = P(X \le x) = \sum_{k=0}^x P(X = k) = \sum_{k=0}^x p(k) $$
이산값일때의 PDF 계산 예제는 아래와 같다.
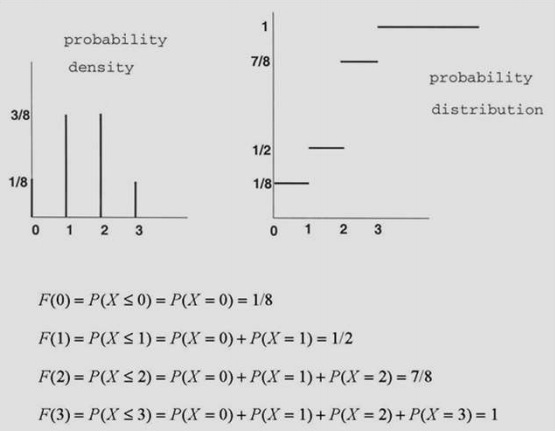
X가 연속값이면 아래와 같이 x까지 적분한다.
$$ F(x) = \int_{-\infty}^x p(t)dt \ for \ all \ x $$
p(x)의 정의는 당연히 F(x)를 미분한 함수이다.
또한 이 의미는 PDF 함수의 미분을 통해 pdf함수를 얻을수 있음을 의미한다.
어차피 pdf를 적분하여 얻는게 PDF 함수이니 당연한 말이긴 하다.
$$ p(x) = \frac {dF}{dx}(x) $$
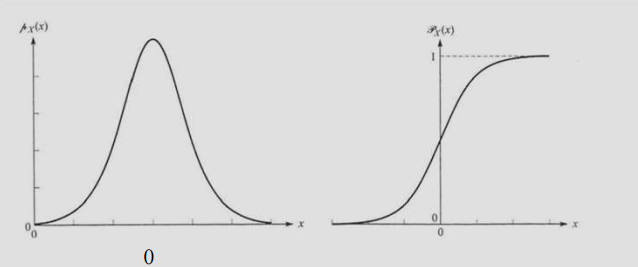
결합 확률 분포(Joint pmf), 이산값일때
확률변수 n에 대해 아래의 수식이 만족한다.
$$ \sum_{x_1,x_2,…,x_n} p(x_1,x_2,…,x_n) = 1 $$
여기서 결합 확률 분포라 함은 2개 이상의 확률 변수에 대해 수식 계산을 하는 방법이다.
(사실 위 수식은 n이 1이어도 결함이 없지만 joint 개념은 2개 이상 사용하긴 한다.)
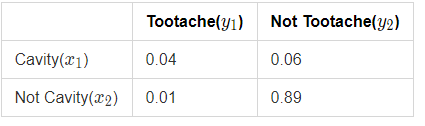
헷갈리니 확률 변수가 $x_1$, $x_2$, …, $x_n$이 아니라 충치여부는 $X$이고 치통은 $Y$라고 가정해보자. 충치일때는 $x_1$, 충치가 아닐때는 $x_2$, 치통이면 $y_1$, 치통이 아니면 $y_2$라고 정해보자. 여기서 위의 수식의 의미는 전체 확률(즉, 1)은 아래의 수식으로 구할수 있다는 뜻이다.
$ p(x_1,y_1) + p(x_2,y_1) + p(x_1,y_2) + p(x_2,y_2) = 0.04 + 0.01 + 0.06 + 0.89 = 1 $
결합 확률 분포(Joint pmf), 연속값일때
연속 확률변수일때는 $p(x_1,x_2,…,x_n) \ge 0 $ 일때 joint pdf는 아래와 같다.
즉 위의 원리에서 연속값이니 적분을 이용하는 것만이 차이점이다.
$$ \int_{x_1}…\int_{x_n}p(x_1,x_2,…,x_n)dx_1…dx_n = 1 $$
조건부 pdf(coditional pdf)
조건부 pdf는 아래의 조건부 확률 수식을 이용하여 아래와 같이 유도할 수 있다.
$ p(y|x) = \frac {p(x,y)}{p(x)} $
$ p(x,y) = p(y|x)p(x) $
$ p(x_1, x_2,…, x_n) = p(x_1|x_2,…,x_n)p(x_2|x_3,…,x_n)…p(x_{n-1}|x_n)p(x_n)$
조금더 쉽게 이해하자면 $ p(x,y) = p(y|x)p(x) $ 이 수식을 이용하기 위해 $x_1$을 우선 $y$, 나머지를 $x$로 치환했다고 생각해보자.
치환을 이용해 전개하면 아래와 같이 된다.
$p(y|x)p(x) = p(x_1|x_2,…,x_n)p(x_2,x_3,…,x_n)$
다시 같은 방법으로 p(x_2,x_3,…,x_n) 에서 $x_2$를 $y$, 나머지를 $x$라 치환해보자.
$p(y|x)p(x) = p(x_1|x_2,…,x_n)p(x_2|x_3,…,x_n)p(x_3,…,x_n)$
이를 연쇄법친으로 끝까지 가면 더이상 for-loop 돌듯이 마지막 변수 2개가 남을때 까지 갈 것이고 그건 $p(x_{n-1},x_n)$ 까지 일것이다. 그럼 이를 이용하면 최종적으로 아래와 같이 된다.
$p(y|x)p(x) = p(x_1|x_2,…,x_n)p(x_2|x_3,…,x_n)…p(x_{n-1},x_n)$
독립
확률 변수간 독립일 경우 수식이 간단해진다.
$ p(x,y) = p(x)p(y) $
왜냐하면 $p(x|y)$가 $p(x)$랑 같기 때문이다.
전체 확률의 법칙(Law of Total Probability)
전체 확률은 조건부 확률의 합으로 표현할 수 있다.
$ p(y) = \sum_x p(y|x)p(x) $
Marginalization
주어진 joint pmf/pdf에서 Marginalization을 이용하여 확률변수의 어떤 부분 집합도 계산할 수 있다.
아래 수식을 보면 확률 $p(x)$는 $p(x,y)$의 모든 확률값을 더하면 $p(x)$가 나온다는 것이다.
$ p(x) = \int_{-\infty}^\infty p(x,y)dy $
추상적이니 구체적으로 얘기하자면 바로 밑의 예제 풀어보기의 그림을 참고하여 설명을 하겠다.
아래와 같이 수식을 세우면 이해가 좀 더 편하다.
$ p(x_{x=x_1}) = \int_{-\infty}^\infty p(x_{x=x_1},y)dy $
위 수식은 x가 $x_1$ 일때의 확률은 $p(x_{x=x_1},y)$의 확률의 합이랑 같다는 것이다.
즉 이는 다시 풀이하면 $ p(x_{x=x_1}) = p(x_{x=x_1},y_{y=y_1}) + p(x_{x=x_1},y_{y=y_2}) $로 나타낼 수 있다.
아래 그림에서 이는 $ 0.3 = 0.2 + 0.1 $이니 참인것을 알 수 있다.
다시 돌아와 $ p(x) = \int_{-\infty}^\infty p(x,y)dy $는 아래와 같이 된다.
$ p(x) = p(x_{x=x_1},y_{y=y_1}) + p(x_{x=x_1},y_{y=y_2}) + p(x_{x=x_2},y_{y=y_1}) + p(x_{x=x_2},y_{y=y_2}) + p(x_{x=x_3},y_{y=y_1}) + p(x_{x=x_3},y_{y=y_2}) $
이를 검증하면 아래와 같이 된다.
$ 1.0 = 0.2 + 0.1 + 0.1 + 0.2 + 0.1 + 0.3 $
수식에서 $y$자리에 $x_2, …, x_n$을 치환하면 아래와 같은 수식이 된다.
$$ p(x_1,x_2,…,x_{i-1}, x_{i+1}, …, x_n) = \int_{-\infty}^\infty p(x_1,x_2,…,x_n)dx $$
$$ p(x_1,x_2) = \int_{x_3} … \int_{x_n} p(x_1,x_2,…,x_n)dx_3…dx_n $$
예제 풀어보기
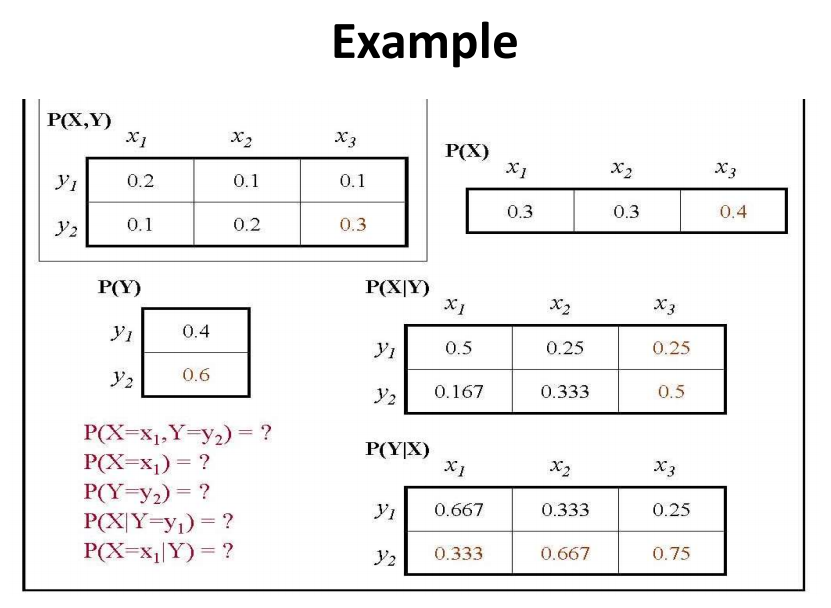
$ P(X=x_1, Y=y_2) = ? $
위 표에 의해서 $ 0.1 $
$ p(X=x_1) = ? $
$ p(X=x_1) = 0.3 $
$ p(X=x_1) = ? $
$ p(Y=y_2) = 0.6 $
$ P(X|Y=y_1) = ? $
$ P(X|Y=y_1) = P(x_1|y_1) + P(x_2|y_1) + P(x_3|y_1) = 1.0$
$ P(X=x_1|Y=Y) = ? $
$ P(X=x_1|Y=Y) = P(x_1|y_1) + P(x_1|y_2) = 0.5 + 0.167 $
정규분포(Normal Distiribution)
정규분포의 pdf는 아래와 같이 정의된다.
$ p(X) = \frac {1}{\sigma \sqrt {2\pi}} exp[\frac {-(x-\mu)^2}{2\sigma^2}] $
$ \mu$는 평균을 의미하고 $\sigma$는 표준편차를 의미한다.
d 차원에서는 수식이 아래와 같아진다.
$ p(X) = \frac {1}{(2\pi)^{d/2}|\sum|^{1/2}} exp[-\frac{1}{2}(X-\mu)^t\sum^{-1}(X-\mu)] $
파라미터와 shape의 가우시안 분포는 아래와 같다.
- 파라미터는 $ d+ \frac {d(d+1)}{2} $이다.
- $\mu$에 의해 정의된 위치, $\sum$에 의해 정의된 shape
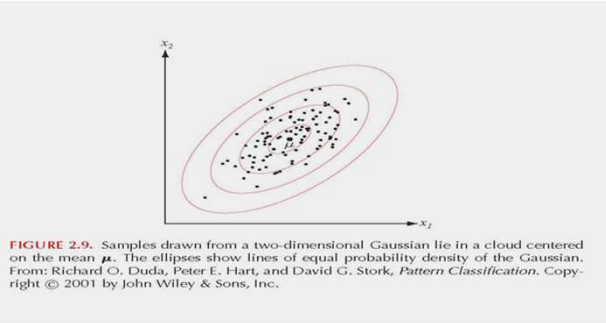
$ p(X) = \frac {1}{(2\pi)^{d/2}|\sum|^{1/2}} exp[-\frac{1}{2}(X-\mu)^t\sum^{-1}(X-\mu)] $ 에서
Mahalanobis distance는 아래와 같다.
$ r = (X – \mu)^t \sum^{-1} (X – \mu) $
만약 변수들이 독립적이면 다변수 정규분포는 아래와 같아진다.
($\sum$은 diagonal)
$$ p(X) = \Pi_i \frac {1}{ \sqrt {2\pi\sigma_i^2}} exp[\frac {-(x_i-\mu_i)^2}{2\sigma_i^2}] $$
기대값(Expected Value)
이산값의 기대값 계산은 아래와 같다.
$ E(X) = \sum_x xp(x) $
예를 들어 주사위의 기대값은 아래와 같이 된다.
표본평균값 $\bar x$는 아래와 같다. 즉 단순 $x$개의 평균이다.
$$\bar x = \frac {1}{x} \sum_{i=1}^n x_i$$
이부분이 완전히 이해가 되지 않지만 필자의 해석은 데이터가 많으면 많아질수록 기대값은 평균값에 가까워진다는 의미인듯 하다.
$$ E(X) = \lim_{n->\infty} \bar x $$
연속값의 기대값은 아래와 같다.
$$ E(X) = \int_{-\infty}^\infty xp(x)dx $$
분산과 표준편차(Variance, Standard Deviation)
분산의 정의는 아래와 같다.
$\mu = E(X)$일때, $ Var(X) = E((X – \mu) ^2) = \sum (X-\mu)^2p(x) $
참고한 자료에 $\mu=E(X)$라는 내용이 있는데 역시 필자의 조심스런 해석은 데이터가 많으면 $\mu$자리에 $E(X)$가 들어갈 여지가 있다고 이해하고 있다.
표본 분산은 아래와 같이 정의된다.
$ \bar{Var(X)} = \frac {1}{n-1} \sum_{i=1}^n(x_i-\bar x)^2$
표준 편차의 정의는 아래와 같다.
$ \sigma = \sqrt{Var(X)} = \sqrt{\sum (X-\mu)^2p(x)}$
공분산
두 확률변수 X와 Y사이의 공분산 정의는 아래와 같다. 각각의 표본을 각각의 평균값으로 빼준 후 기대값을 구하는 것이다.
$ \mu_x = E(X), \mu_Y = E(Y) $ 이면 $Cov(X,Y) = E((X-\mu_X)(Y-\mu_Y)) $
X와 Y의 상관계수(Correlation Coefficient)는 아래와 같이 구할 수 있다.
$$p_{XY} = \frac {Cov(X,Y)}{\sigma_X\sigma_Y}$$
공분산 행렬 – 2개 변수(Covariance Matrix)
X와 Y에 대한 공분산 행렬은 아래와 같이 정의된다.
$ \sum = C_{XY} = \begin{bmatrix} Cov(X,X) & Cov(X,Y) \ Cov(Y,X) & Cov(Y,Y) \end{bmatrix}$
표본 공분산 행렬은 아래와 같이 계산 될 수 있다.
$$ Cov(X,Y) = \frac {1}{n-1} \sum_{i=1}^{n-1} (x_i – \bar x)(y_i – \bar y)$$
n개의 확률변수에서의 공분산 행렬은 아래와 같다.
$ C_{X} = \begin{bmatrix} Cov(X_1,X_1) & Cov(X_1,X_2) & … & Cov(X_1,X_n) \ Cov(X_2,X_1) & Cov(X_2,X_2) & … & Cov(X_2,X_n) \ … & … & … & … \ Cov(X_n,X_1) & Cov(X_n,X_2) & … & Cov(X_n,X_n) \end{bmatrix}$
Uncorrelated Random Variable
X와 Y가 uncorrelated이면 아래 수식이 성립한다.
$ Cov(X,Y) = 0 $
$ X_1, X_2, …, X_n$ 이 uncorrelated이면 아래 수식이 성립한다.
$ C_X = D $, $D$ is diagonal matrix.
공분산 행렬의 속성
- $C_X$가 symmetric하기 때문에, real eigen value는 0보다 크거나 같다.
- 서로 다른 고유값 구성된 아무 2개의 고유벡터는 기저로 정의된다.
(대각화의 조건이 서로 다른 고유값으로 구성되는 것이고 대각화면 벡터들이 기저이니까 이 케이스에서는 고유벡터들이 기저이다. ) - 두개의 다른 고유값으로 구성된 고유벡터는 orthogonal한다.
(바로 위 정의에서 각 고유벡터가 기저라고 했으나 당연이 orthogonal하다.)
공분산 행렬 분해
행렬대각화가 가능하니 아래와 같이 정의할 수 있다.
$ C_X = \emptyset \Lambda \emptyset^{-1} $ where $ \emptyset^{-1} = \emptyset ^T$
- $ \emptyset $의 column은 $C_X$의 고유벡터이다.
- $ \Lambda $의 diagonal element는 $C_X$의 고유값이다..
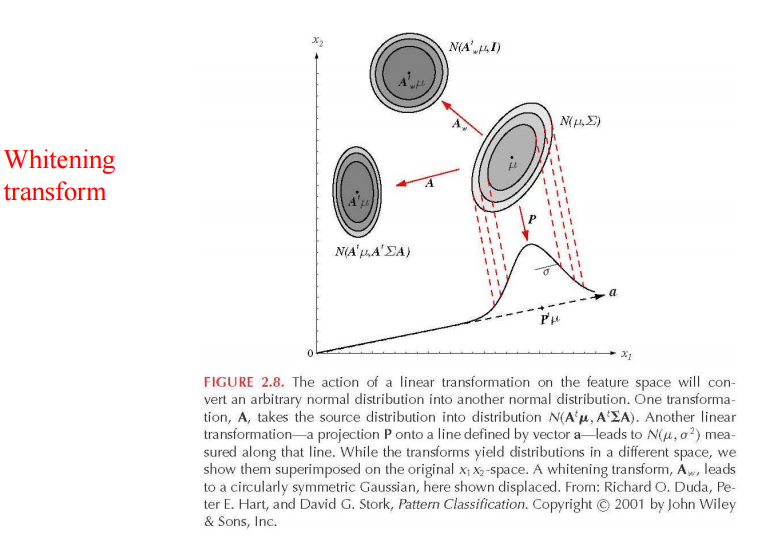
선형변환
만약 $ y = A^t X$이면 $p(y) \simeq N(A^t\mu,A^t \sum A) $이다.
whitening transformation 정의는 아래와 같다.
$ A_w = \emptyset \Lambda^{-1/2}$
만약 $ y = A^t_w X $이면 $ p(y) \simeq N(A^t_w\mu,I) $이고 즉 $\sum_w = I$이다.
$\emptyset$은 orthonormal한 eigenvector 의 $\sum$이고 $\Lambda$는 eigenvalue의 $\sum$에 상응하는 diagonal matrix이다.