개요
필자가 정리한 내용에 오류가 있을수 있음을 염두해두고 비판적으로 내용정리를 참고했으면 한다.
PCA의 개념 익히기
시작이 반이라는 얘기가 있듯이 PCA는 개념과 목적을 이해하면 반은 이해한다고 봐도 무방할듯 하다.
아래와 같이 X라는 2차원 벡터가 있다고 가정해보자.
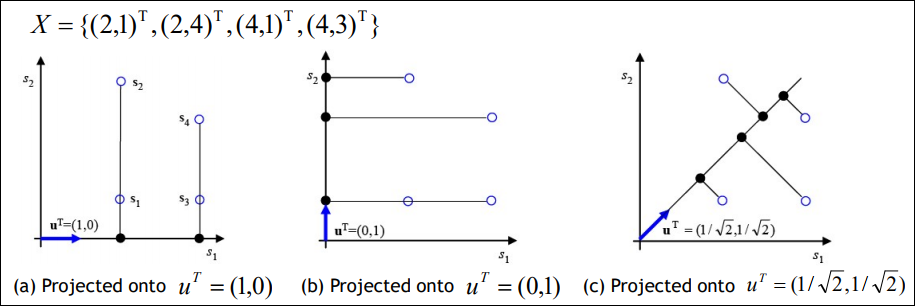
X의 각각의 벡터 $(2,1), (2,4), (4,1), (4,3)$은 $s_1, s_2, s_3, s_4$에 해당한다.
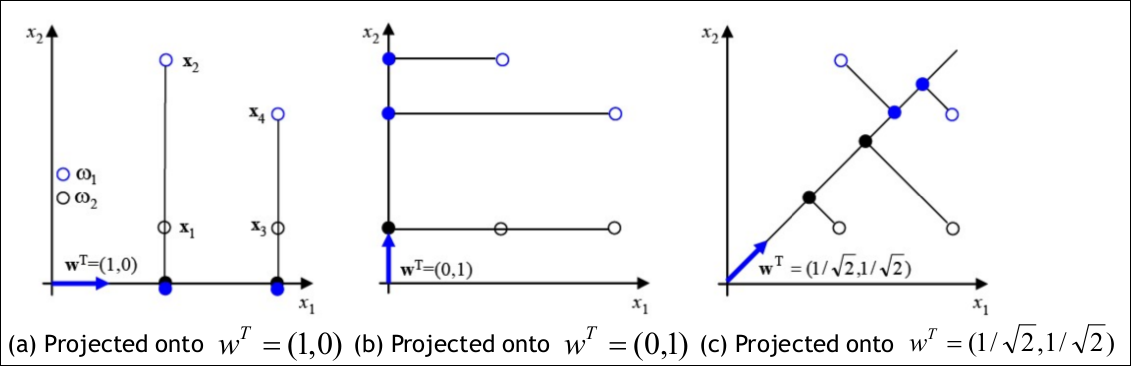
이 벡터들을 $ u$라고 하는 벡터에 의해 projection한다고 가정해보면 $u$ 벡터가 아래와 같이 a, b,c값일때 각각 projection 되는 방식은 아래와 같아진다.
여기서의 의미가 중요한데 projection의 효과는 아래와 같이 2차원 벡터들이 1차원의 공간으로 사상되어 차원이 축소되는 효과를 가진다. (a) 케이스를 예로 들면 X벡터가 ${(2,0),(4,0)}$ 으로 바뀌어 1차원의 값만 가진다.
PCA의 목적은 최소한의 loss를 가지고 정보를 압축하는 것이다.
이를 달리 얘기하면 가장 높은 분산을 가지는 차원으로 축소를 수행하는 것이다.
가장 높은 분산을 가지는 것이 loss가 최소화 되는 이유는 아래와 같다.
위의 그림에서 a~c의 그림을 보면 상대적으로 분산은 c가 제일 크다. 우리가 머신러닝에서 classification 문제를 생각해본다면 data끼리 분류가 되어야 하는데 a~b는 4개의 데이터가 2개로 합쳐지고 분산도 작다. 반면에 c는 데이터가 한 축으로 합쳐지더라도 4개가 구별되고 분산이 크다. 따라서 좋은 차원 축소라 하면 차원은 줄어들더라도 분산이 커서 각각의 데이터가 구별이 되어야 이후에 training을 돌릴때 유리할 것이다. 즉 분산이 작으면 데이터 간의 특징점이 없어지거나 약해질 가능성이 높다. 따라서 PCA는 항상 축을 찾을때 분산이 큰것부터 작은 순으로 찾는다.
분산값 구해보기
그렇다면 실제로 a와 c의 평균 및 분산값을 한번 구해보자.
$ s_1 = (2,1)^T, s_2 = (2,4)^T, s_3 = (4,1)^T, s_4 = (4,3)^T $
$u$에 의해 선형변환 되는 $X$를 $ \hat{X} = u^T s$로 수식을 세워보자.
계산해보면 실제로 c 케이스가 분산이 더 큰것을 알 수 있다.
(a) 케이스
$\hat{x_1} = \begin{pmatrix} 1 & 0 \end{pmatrix} \begin{pmatrix} 2 \\ 1 \end{pmatrix} = 2, \ \hat{x_2} = \begin{pmatrix} 1 & 0 \end{pmatrix} \begin{pmatrix} 2 \\ 4 \end{pmatrix} = 2, \ \hat{x_3} = \begin{pmatrix} 1 & 0 \end{pmatrix} \begin{pmatrix} 4 \\ 1 \end{pmatrix} = 4, \ \hat{x_4} = \begin{pmatrix} 1 & 0 \end{pmatrix} \begin{pmatrix} 4 \\ 3 \end{pmatrix} = 4$
$ Mean = 3, Variance = 1$
(c) 케이스
$\hat{x_1} = \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \frac{3}{\sqrt{2}}, \ \hat{x_2} = \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 2 \\ 4 \end{pmatrix} = \frac{6}{\sqrt{2}}, \ \hat{x_3} = \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 4 \\ 1 \end{pmatrix} = \frac{5}{\sqrt{2}}, \ \hat{x_4} = \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 4 \\ 3 \end{pmatrix} = \frac{7}{\sqrt{2}}$
$ Mean = 3.7123, Variance = 1.0938$
$u$를 어떻게 구할것인가?
그렇다면 선형변환 시 가장 큰 분산이 되는 $u$를 어떻게 구할 수 있을까?
그전에 Notation을 한번 정리하고 가보자.
Mean of ${\hat{x_1}, …, \hat{x}_{N}} $
$=$ $ \bar{\hat{x}} $
$ = \frac{1}{N} \sum_{i=1}^N \hat x$
$ = \frac {1}{N}\sum_{i=1}^N u^Ts$
$ =u^T(\frac {1}{N}\sum_{i=1}^N s_i) $
$ = u^T \bar{s} $
위 수식에서 주목할 점은 평균의 경우 각각의 projection의 평균은 평균의 projection과 같다는 것을 알 수 있다. 따라서 이 것을 분산을 구할 때 이용한다.
$u^T(\frac {1}{N}\sum_{i=1}^N s_i) = u^T \bar{s}$
Variance of ${\hat{x_1}, …, \hat{x}_{N}}$
$ = \hat\sigma = \frac{1}{N} \sum_{i=1}^N (\hat x_i – \bar{\hat{x}})^2 $
$ = \frac {1}{N}(u^T s_i – u^T \bar s)^2$
우리의 목적은 분산 $\hat\sigma$를 최대화 하는 $u$를 찾는것이다.
이런 문제에서의 최대 최소는 보통 극점에서 발생하기 때문에 극점에서 접선이 맞닿는 case를 찾기위해 편미분을 통해 최대 또는 최소를 구하는 라그랑주 승수법으로 해결 할 수 있다. 이를 라그랑주 승수법을 이용하여 수식을 목적함수를 만들면 아래와 같다. (여기서 $u^Tu = 1$이라는 제약조건을 추가해보자. 이부분에 대한 이유는 필자도 모르겠다.)
$ L(u) = \frac {1}{N} \sum_{i=1}^N (u^Ts_i – u^T\bar{s})^2 + \lambda(1-u^Tu) $
위 수식의 해는 아래와 같이 각각 풀 수 있다.
$ \frac {\partial{L(u,\lambda)}} {\partial u} = 0 $ or $ \frac {\partial{L(u,\lambda)}} {\partial\lambda} = 0 $
여기서 $ \frac {\partial{L(u,\lambda)}} {\partial\lambda} = 0 $의 경우 $u^Tu = 1$가 되고 이건 우리가 정했던 제약조간이니 결국 $ \frac {\partial{L(u,\lambda)}} {\partial u} = 0 $만 구하면 된다.
라그랑주 해법 수식유도
아래의 유도는 사실 결론만 알아도 된다.
$ \frac {\partial L(u)}{\partial u} = \frac {\partial{(\frac {1}{N} \sum_{i=1}^N (u^Ts_i – u^T\bar{s})^2 + \lambda(1-u^Tu))}}{\partial u} = 0$
$ = \frac{2}{N} \sum_{i=1}^N (u^Ts_i – u^T\bar{s})(s_i-\bar s)-2\lambda u $
$ = 2u^T (\frac{2}{N} \sum_{i=1}^N (s_i – \bar{s})(s_i – \bar{s}))-2\lambda u$
$ = 2u^T\sum – 2\lambda u $
$ = 2\sum u – 2\lambda u = 0$
즉 정리하면 아래와 같다.
$ \sum u = \lambda u $
여기까지 오면 눈치챈 사람이 있겠지만 이것은 공분산에 대한 아이겐벡터와 아이겐벨류(고유벡터와 고유값)이 된다.
$u$는 $\sum$ (공분산 행렬)에 대한 아이겐벡터(고유벡터)이다. 즉 공분산의 아이겐 벡터와 아이겐 벨류를 구하면 PCA를 수행할 수 있다.
PCA 예제로 구해보기
$X$ = {$(2,1)^T, (2,4)^T, (4,1)^T, (4,3)^T$}
위의 X의 공분산을 구해보자.
공분산 행렬은 아래와 같이 구성된다.
$ \sum = \begin{pmatrix} Cov(X,X) & Cov(X,Y) \\ Cov(Y,X) & Cov(Y,Y) \end{pmatrix} $
계산해보면 X의 평균값은 3, 분산은 1이다. 또한 Y의 평균값은 2.25이고 분산은 1.688이다.
마찬가지로 $Cov(X,Y)$를 계산해보면 -0.250이다. 이를 정리하면 아래와 같다.
$\sum = \begin{pmatrix} 1.000 & -0.250 \\ -0.250 & 1.6888 \end{pmatrix} $
이 공분산을 가지고 아이겐 벨류와 아이겐 벡터를 구하면 아래와 같다.
해당값을 구하는 방법은 링크를 참고하자.
$ \lambda_1 = 1.76888, \ u_1^T = (-0.3092, 0.9510)$
$ \lambda_2 = 0.9187, \ u_2^T = (-0.9510, -0.3092)$
$u_1^T$로 $X$를 projection 해보자.
$\hat{x_1} = \begin{pmatrix} -0.3092 & 0.9510 \end{pmatrix} \begin{pmatrix} 2 \\ 1 \end{pmatrix} = 0.3326$
$\hat{x_2} = \begin{pmatrix} -0.3092 & 0.9510 \end{pmatrix} \begin{pmatrix} 2 \\ 4 \end{pmatrix} = 3.1856$
$\hat{x_3} = \begin{pmatrix} -0.3092 & 0.9510 \end{pmatrix} \begin{pmatrix} 4 \\ 1 \end{pmatrix} = -0.2858$
$\hat{x_4} = \begin{pmatrix} -0.3092 & 0.9510 \end{pmatrix} \begin{pmatrix} 4 \\ 3 \end{pmatrix} = 1.6162$
$Mean = 1.2122, \ Variance=1.7688$
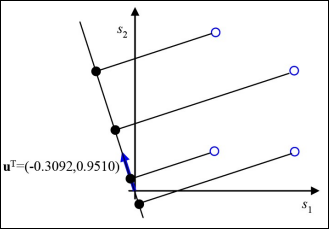
따라서 아래와 같은 projection이 수행되고 분산이 이때까지 구한것보다 더 크다.(실제로 최대이다.)
고유값의 특징
공분산을 통해 구한 고유값은 $\lambda$값이 클수록 분산이 크다. 또한 $\lambda$의 성질이 점차 급격하게 수렴하는 성질이 있다. 따라서 이를 이용하여 적절한 $\lambda$의 갯수를 찾을 수 있는데 이게 곧 적절히 축소될 차원을 의미한다.(람다의 갯수가 곧 차원의 갯수이다.)
PCA 알고리즘
이때까지 설명한 PCA를 알고리즘으로 만든다면 아래와 같다.
입력값 : $X=${$s_1,s_2,…,s_N$}, d(원하는 차원)
출력값 : projection 행렬 U, 평균 벡터 $\bar s$
- $X$의 평균 벡터를 계산한다. $X = \bar s = \frac {1}{N} \sum_{i=1}^N s_i$
- 표본 평균을 구한다. for ($i$=1 to $N$) s’$_i = s_i – \bar s$
- 공분산 행렬 $\sum$을 구한다.
- $\sum$의 고유벡터와 고유값을 구한다.
- 고유값이 큰 순서대로 $u_1, u_2, …, u_d$를 구한다.
- projection 된 행렬 $U$를 구한다.
PCA를 이용한 어플리케이션
- Feature Extraction
- Face recognition(eigenface, MIT에서 처음 만들었는데 획기적이었음)
- 차원 축소
- 데이터 압축 및 복원(projection을 반대로 하면 복원)
- 데이터 시각화
이미지 classification 예제로 풀어보기
머신러닝 문제에서 이미지를 분류 할 때 아무래도 요즘 이미지가 4K시대에 이르러 엄청나게 커지는 이슈가 있다. 아무리 딥러닝 시대라고 해도 curse of dimesion의 문제는 완벽히 해결되었다기 보다 아직 고민해야 되는 문제이다. 이때 PCA를 적용하면 어떻게 차원이 축소되고 도움이 되는지 예제로 알아보자.(PCA가 만능의 해결책이란 뜻은 아니다.)
아래의 예제에서 $x^1 $ ~ $x^4$ 중에서 $y^1$과 가장 비슷한 그림을 찾아보려고 한다.

위 문제에 알고리즘을 적용해보자.
1.우선 각 이미지의 벡터는 아래와 같고 평균값 벡터 $m$을 구한다.

- 표본 평균을 구한다.
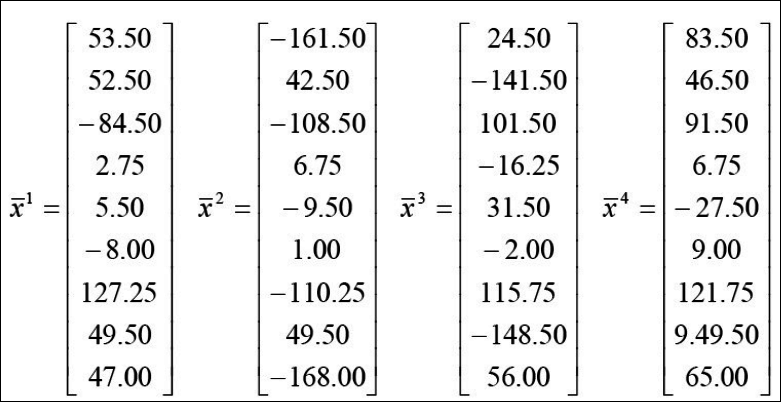
- 공분산 행렬 $\sum$을 구한다. $\Omega$라고 표시된 것이 $\sum$이다. 위의 x1~x4밑 각 9차원의 벡터의 값과 아래의 행렬의 크기가 헷갈릴 수 있다. X는 x1~x4를 합친 94이과 $\bar X$는 4 * 9이다. 따라서 이걸 곱하고 나면 99크기가 된다. 공분산 개념은 cov(x의1차원,x의 1차원) cov(x의1차원,x의 2차원) … cov(x의1차원,x의 9차원) cov(x의2차원,x의 1차원) cov(x의2차원,x의 2차원) … cov(x의2차원,x의 9차원) 이런식의 표현이다.
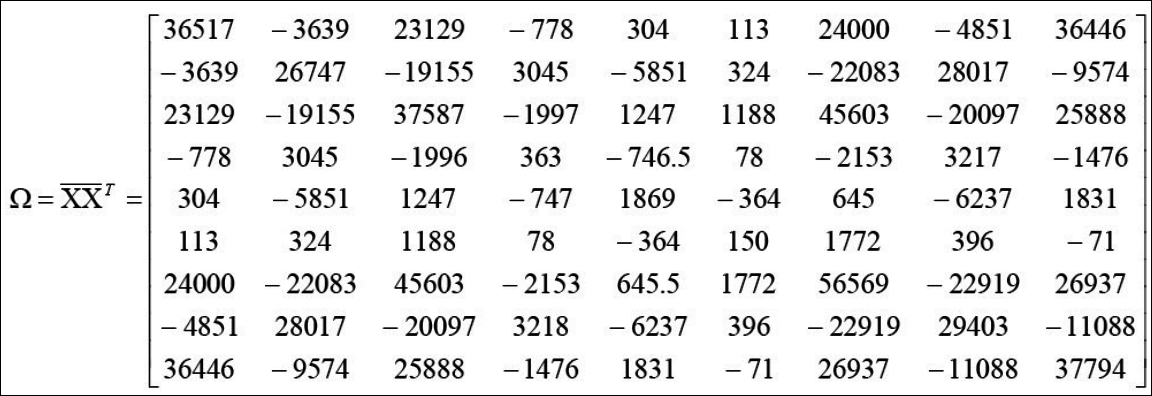
- $\sum$의 고유벡터와 고유값을 구한다.
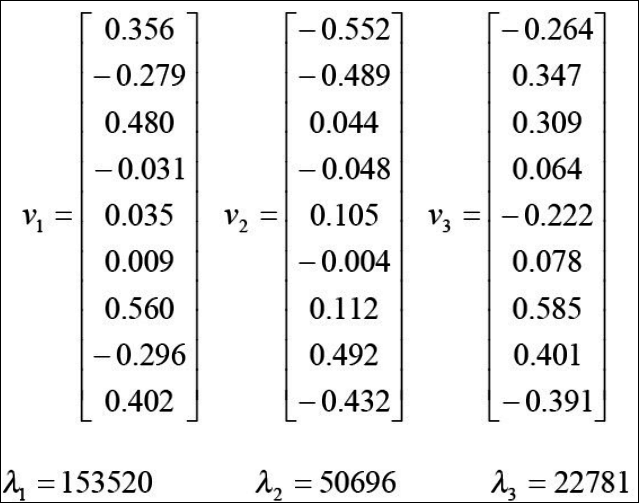
- 고유값이 큰 순서대로 $u_1, u_2, …, u_d$를 구한다.
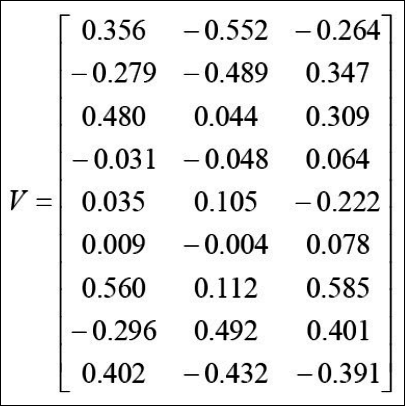
- projection 된 각각의 벡터를 구한다.
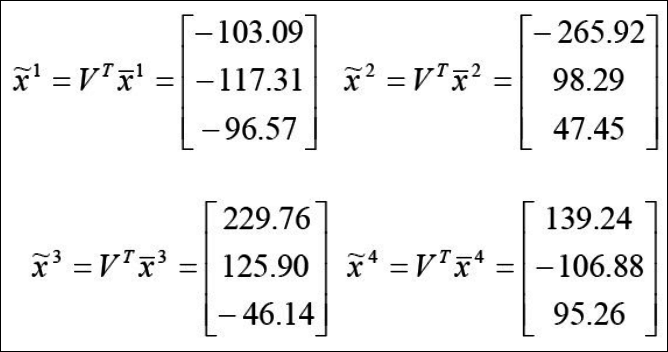
이렇게 까지 했으면 이제 테스트 데이터인 y에 대해 같은 방법으로 계산해보자.

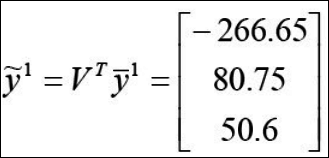
이렇게 구한 y를 x1~x4와 유클리드 거리비교를 해보면 각각 296, 18, 508, 449로 결국 $x_2$랑 $y_1$이 가장 비슷한 것을 알 수 있다. 이중에 $x_2$랑 $y_1$의 유클리드 거리는 아래와 같이 실제 구해보자.
$ \sqrt{(-265.92-(-266.65))^2 + (98.29-80.67)^2 + (47.45-50.6)^2} = \sqrt{318.107} = 17.83 \simeq 18$
eigenface 예제로 풀어보기
- N x N 픽셀의 이미지를 로드한다.
(모든 이미지는 같은 크기이고 중앙의로 얼굴이 정렬되어 있어야 한다.)

- 매 이미지를 벡터로 나타낸다.
($N^2 * 1$ 벡터) - 벡터의 평균을 계산한다.
$ \Psi = \frac {1}{M} \sum_{i=1}^M \Gamma_i $ - 각 값을 평균으로 뺀다.
$ \Phi_i = \Gamma_i – \Psi $ - 공분산 행렬 C를 구한다.
$ C = \frac {1}{M} \sum_{n=1}^M \Phi_n \Phi_n^T = AA^T $ ($N^2 * N^2$ matrix)
이때 $A = \Phi_1 \Phi_2 … \Phi_M $ ($N^2 * M$ matrix)
5번의 각 행렬 크기에 대해 살짝 첨언을 하자면 $\Phi_1$은 기존의 이미지의 열벡터이니 크기가 $N^2$이다. 이게 행을 구성하고 이게 $M$개 만큼 있으니 ($N^2 * M$ matrix)가 된다.
또한 C는 $N^2 * M * M * N^2$이 되니까 $N^2 * M$가 된다. - $AA^T$의 아이겐벡터를 구한다.
여기서 $AA^T$의 경우 $N^2 * N^2$ 이므로 계산량이 많고 효율적이지 못하다. 따라서 trick으로 아래의 수식을 만족하는 아이겐벡터를 구한다.
$ A^TAv_i = \mu_iv_i$
핵심은 위의 식을 만족하는 아이겐 벨류는 $AA^T$의 아이겐 벨류와 같다는 것이다.
이유를 한번 알아보자.
$ A^TAv_i = \mu_iv_i$에서 각변에 $A$를 곱한다.
$u$는 상수이니 $ AA^TAv_i = \mu_i A v_i$로 표현할 수 있다.
여기서 $Av_i$를 $v’$이라고 치환하면 아래와 같은 수식이 된다.
$ AA^Tv’ = \mu_i v’$
즉 고유벡터는 달라지지만 $AA^T$와 $A^TA$의 고유값은 같은것을 알 수 있다.
SVD를 이용한 PCA
$ X = $ {$x^1, x^2, …, x^N$}$ $
-
$ \bar x = \frac {1}{N}\sum_{n=1}^N x^n $를 이용하여 각 point의 평균을 구한다.
$x_c^i = x^i – \bar x $ -
$x_c^i$를 행 벡터로 가지는 Y 행렬을 구성한다.
-
SVD를 돌리면 $ Y = USV^T $를 만족하는 $U,S,V^T$가 구해진다.
$Y,V^T$는 orthogonal, $S$는 diagonal이다.
$ Y = A^T = USV^T$, $ A = VSU^T$ (이유는 $(AB)^T = B^TA^T$ 이기 때문)
이를 이용하여 공분산 행렬을 구해보면 $ C = AA^T = VSU^T USV^T $이다.
이를 계산하면 $C = VS^2V^T$이다.
여기서 $V$를 각변에 곱하면 $CV = VS^2V^T V$이다.
이를 정리하면 아래의 수식이 나온다.
$ CV = S^2V$
S는 결국 아이겐벨류의 제곱이 되므로 SVD를 통해 아이겐벨류를 쉽게 구할 수 있다.
$ S^2 = \begin{bmatrix} \lambda_1^2 & … & … & … \\ … & \lambda_2^2 & … & … \\ … & … & … & … \\ … & … & … & \lambda_n^2 \end{bmatrix}$
PCA의 한계
- PCA는 데이터가 가우시안 분포라는 가정아래 아이겐 벡터의 공분산 행렬을 이용하기 때문에 각각의 독립된 축을 찾을 수 있다.
- PCA의 주요 한계점은 이 기법이 class간의 분류 용이성(separability)이 고려되지 않았다는 것이다.
- PCA는 단순히 각 축의 최대 분산을 구한다.
- 하지만 이 최대의 분산의 각 축이 반드시 class간의 구별을 잘하는 좋은 feature를 뽑아준다는 보장이 없다.
LDA
우리는 이제 차원을 축소하는데 있어 클래스간의 차별성을 최대화 할 수 있는 방향으로 수행하고 싶다.
만약 아래와 같은 두가지 차원 축소가 있다면 어떤것이 더 클래스 구별성이 좋은가? 당연히 2번일 것이다.
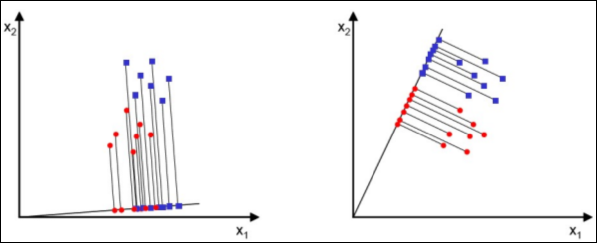
위와 같은 더 좋은 차원 축소를 할 수 있는 기본 개념은 아래와 2가지이다.
- 분리될 class간의 각각의 평균의 거리는 멀수록 좋다.
- 각 class안에서의 분산은 작을수록 좋다.
따라서 이를 수식으로 나타내면 $\frac {|| \bar U_1 – \bar U_2 ||}{\bar S_1^2 + \bar S_2^2}$를 maxmize하면 된다.
이를 그림으로 나타내면 아래와 같다.
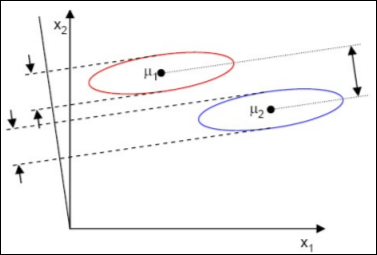
LDA 수식 재정의
우선 위 수식의 분모부터 한번 들여다 보자.
$ S_i = \sum_{s \in w_i}(X – u_i)(X-u_i)^T $
$ S_1 + S_2 = S_w $
여기서 사용된 성질은 $ ||X|| = XX^T $이다.
$ \bar S_i ^2 = \sum_{y \in w_i} (y – \bar u_i)^2 $
$ = \sum_{x \in w_i}(w^TX-w^T\mu_i)^2 $
$ = \sum_{x \in w_i}(w^TX-w^T\mu_i)(w^TX-w^T\mu_i)^T $
$ = \sum_{x \in w_i}w^T(X-\mu_i)(w^T(X-\mu_i))^T $
$ = \sum_{x \in w_i}w^T(X-\mu_i)(X-\mu_i)^Tw = w^TS_iw$
즉 $\bar S_1^2 + \bar S_2^2 = w^TS_ww$이다.
그다음 분자를 한번 들여다 보자.
$ (\bar \mu_1 – \bar \mu_2)^2 = (w^T\mu_1 – w^T\mu_2)^2$
$ = w^T(\mu_1 – \mu_2)(\mu_1-\mu_2)^Tw $
$ = w^TS_Bw$
따라서 Fisher의 criterion에 의한 수식은 아래와 같다.
$ J(W) = \frac {w^TS_Bw}{w^TS_ww} $
LDA 최적화 수식

LDA example
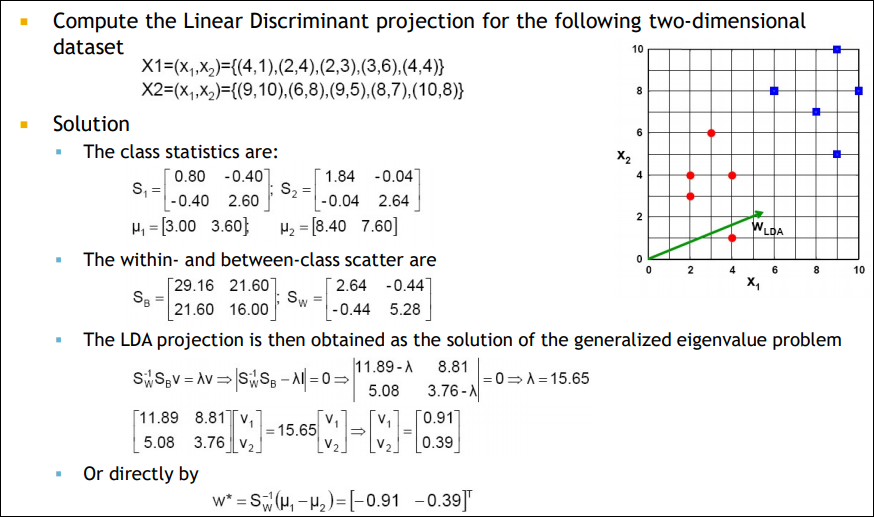
실제로 맞는지 $S_W^{-1}(\mu_{1} – \mu_{2}) $를 계산해보면 아래와 같다. 구해진 벡터를 L2 norm으로 나눠주면 결국 (-0.91, -0.39)가 된다.