개요
회사에서 적용할만한 abusing detection에 대해 공부하기 위해 논문을 좀 살펴보았다. 이중에서 Graph 기반 Knowledge Discovery 알고리즘인 SUBDUE 알고리즘을 공부하고 내용을 정리해본다. 그래프의 MDL을 Unsupervised Learning 으로 학습시킬 수 있다는것이 알고리즘의 핵심이다.
원문링크
링크를 참고하면 된다.
알고리즘 동작 설명
그림을 이용하여 내용을 설명한다.
이 알고리즘은 주어진 그래프를 최대로 압축할 수 있어 그래프를 최소한의 설명(MDL)할 수 있게 만드는 패턴을 찾는것이 목적이다.
최종적으로 알고리즘이 얻고자 하는 것을 먼저 설명한다. 만약 아래와 같은 그래프가 있다고 가정하자.
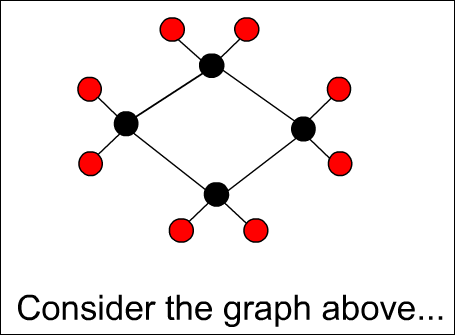
예를 들어 아래의 패턴이 알고리즘에 의해 찾아진 최적의 패턴이라 가정해보자.
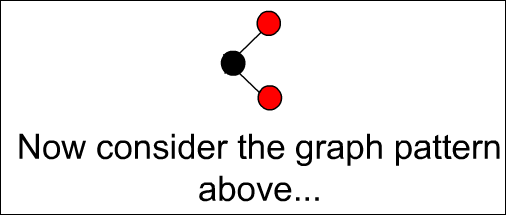
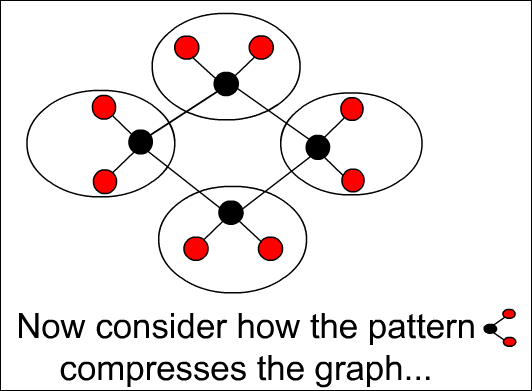
위의 패턴으로 기존의 그래프를 압축을 시도한다. 오른쪽 부분 그래프를 압축한다.
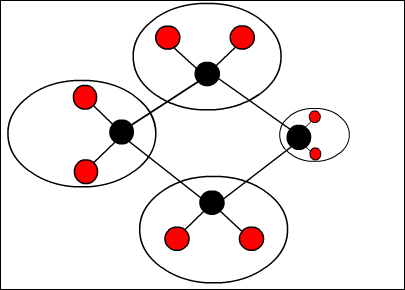
같은 방법으로 왼쪽을 압축한다.
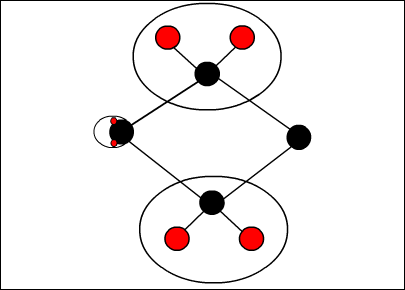
마찬가지로 아래쪽을 압축한다.
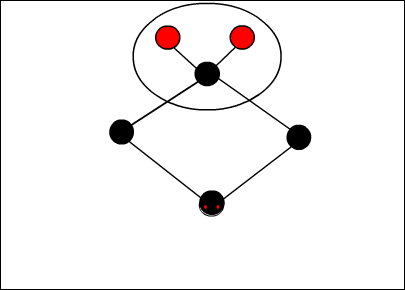
위쪽까지 마저 압축하면 아래와 같은 그래프가 된다. 압축 후의 그래프는 vertex와 edge가 적으면 적을수록 좋다. 즉, 그래프를 최대한 압축할수 있는 부분 그래프를 찾아 이를 통해 기존 그래프를 최소한의 구성으로 설명 할 수 있게끔 하는 것이 이 알고리즘이다.
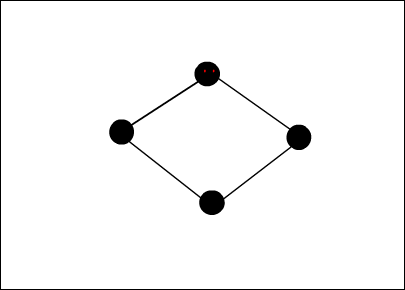
이제 SUBDUE 시스템에서 그래프 패턴(최적의 부분 그래프 패턴)을 어떻게 찾는지 알아보자.

시스템이서 우선 고유한 verticle들을 찾는다.
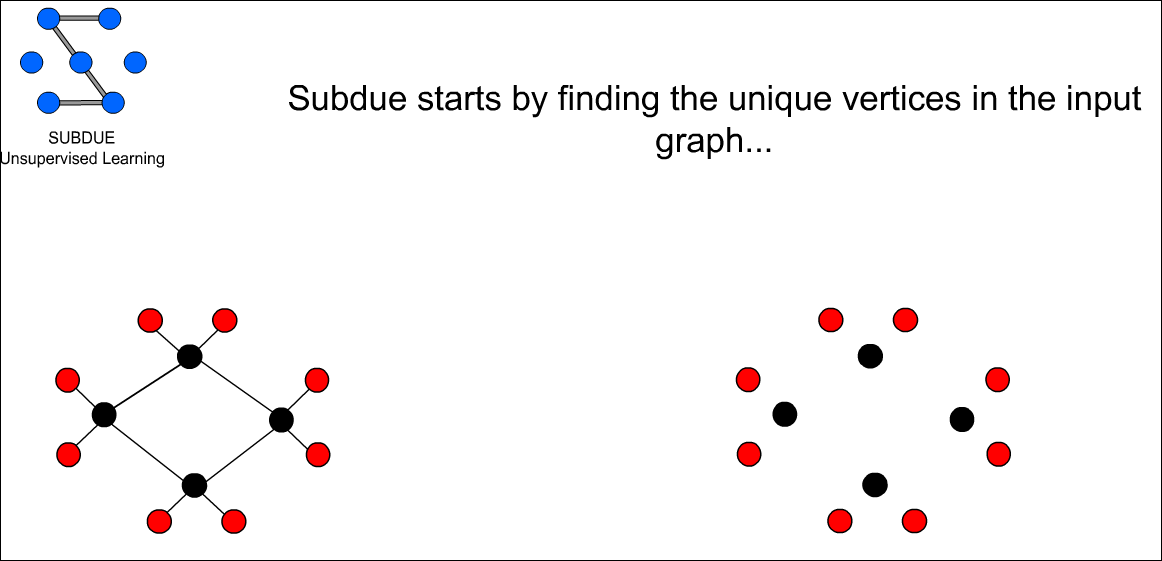
고유한 verticle은 빨간색과 검은색 두 종류이다.
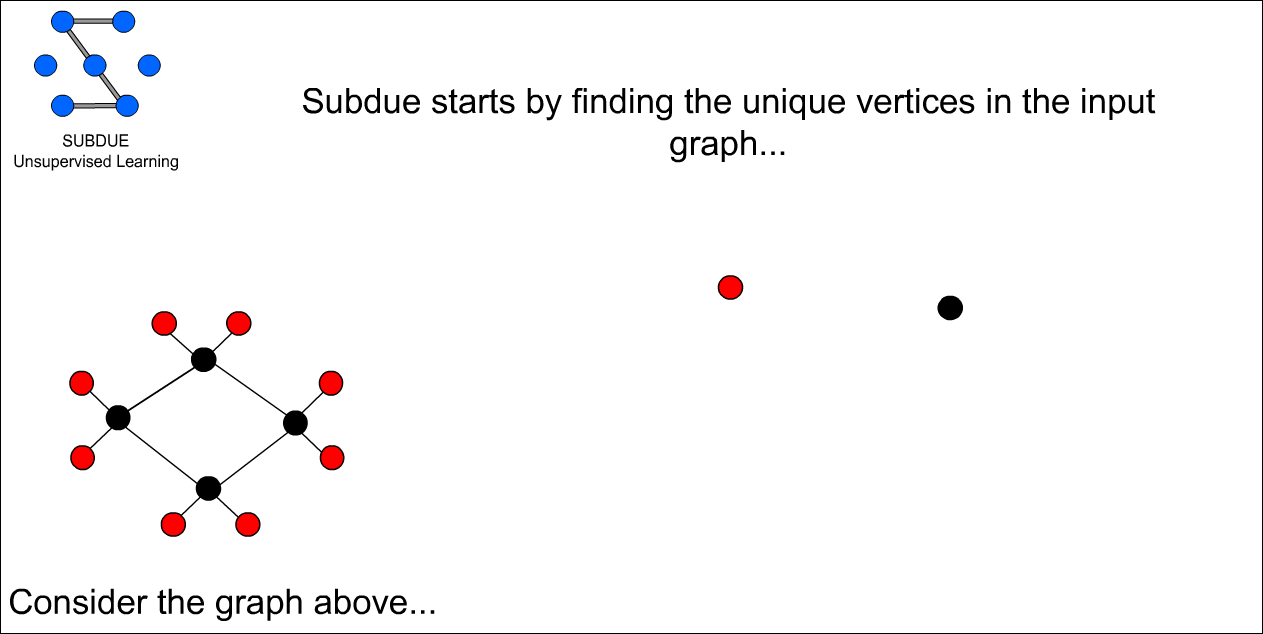
고유 verticle을 edge 하나로 확장 할 수 있는 그래프 패턴을 찾는다.
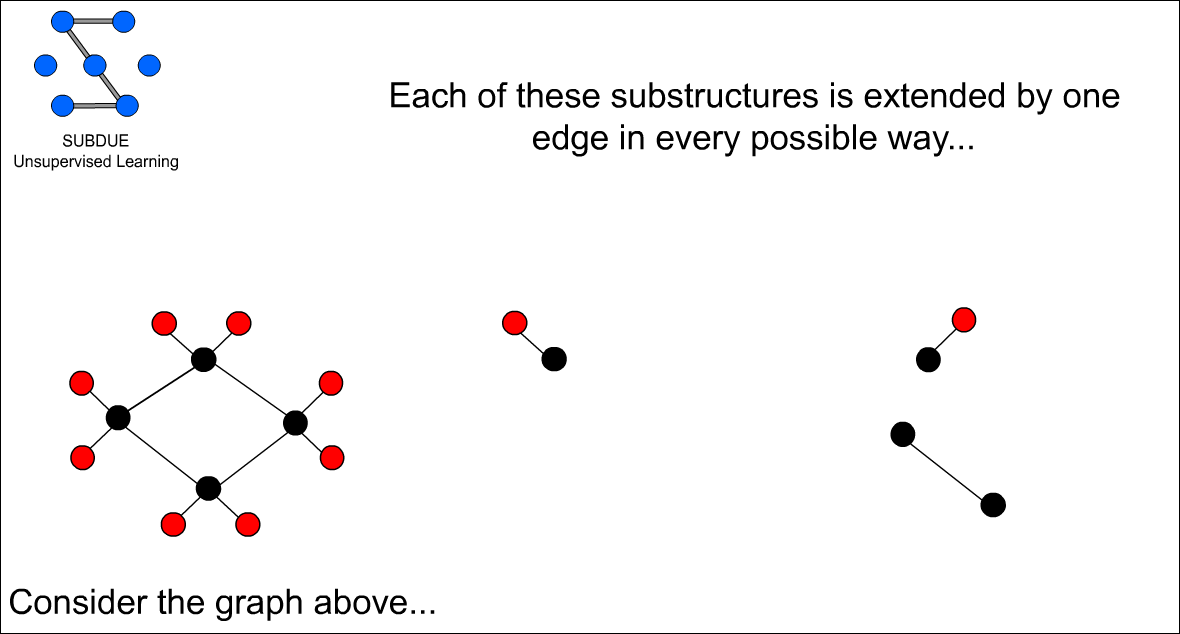
이 그래프 패턴을 다시 unique 한것만으로 추린다.
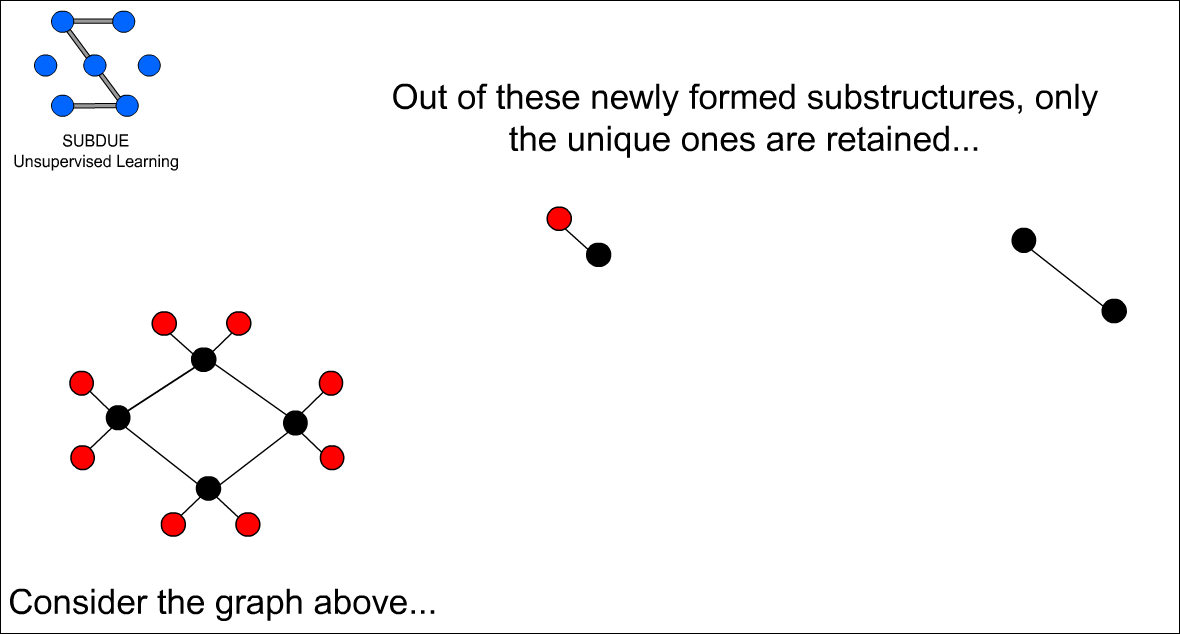
이 부분 구조는 아래의 수식에 의해 평가값을 가진다. 이를 계산해보면 빨간색-검은색으로 구성된 구조는 평가값을 1.26이 되고 검은색-검은색으로 구성된 구조는 1.04가 된다. 이 평가값이 더 큰 단 하나의 구조만을 Best structure(최적의 부분 그래프 패턴) 후보로 취한다.
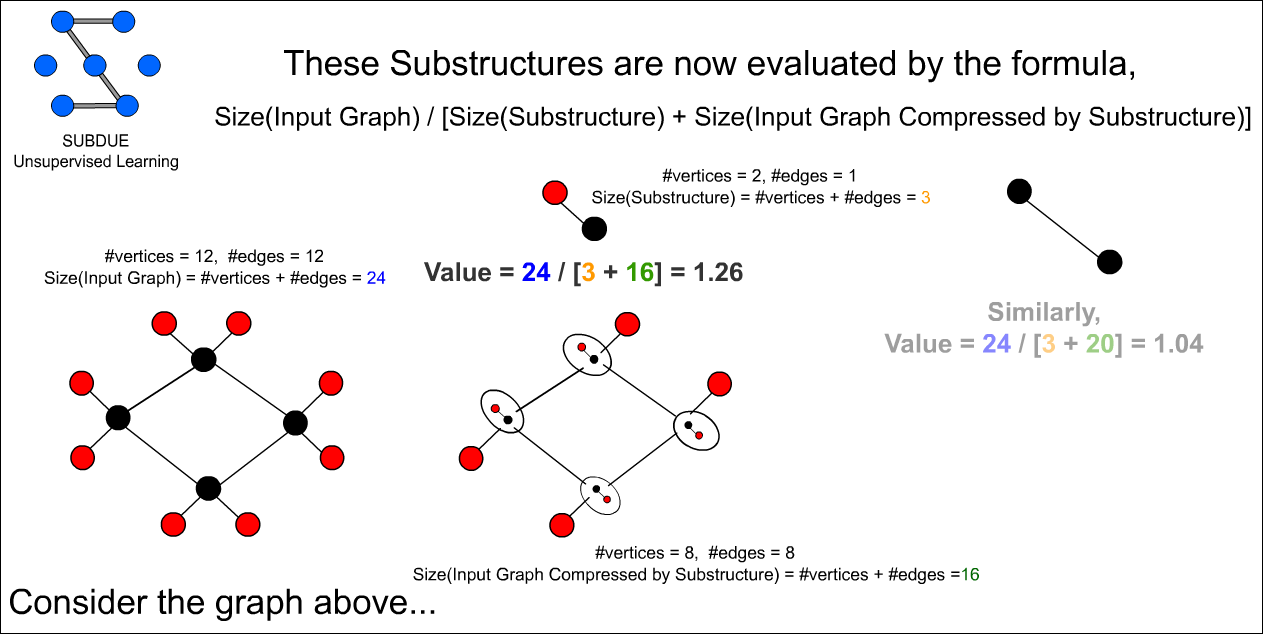
Best structure 후보군을 다시 edge 확장 시도한다.
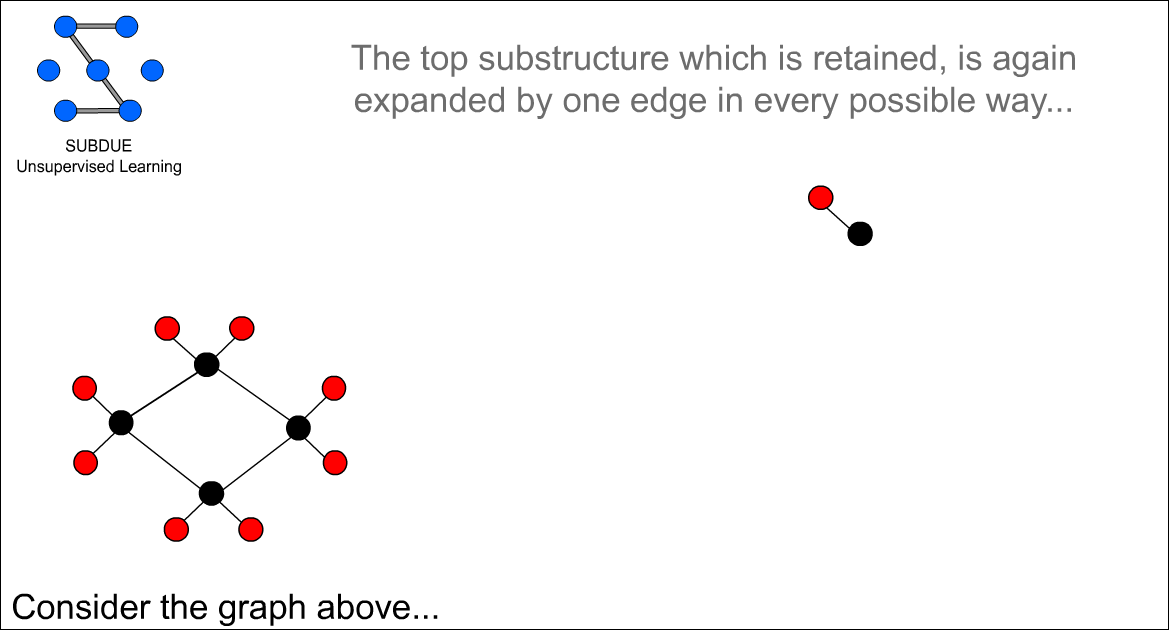
왼쪽의 부분구조는 1.84, 오른쪽의 부분 구조는 1.26이 된다. 기존의 2개였을때의 평가값 까지 포함하여 가장 큰 값을 취하는 그래프 패턴을 best structure로 선정하는데 1.84인 왼쪽의 부분구조가 best structure로 선택 된다.

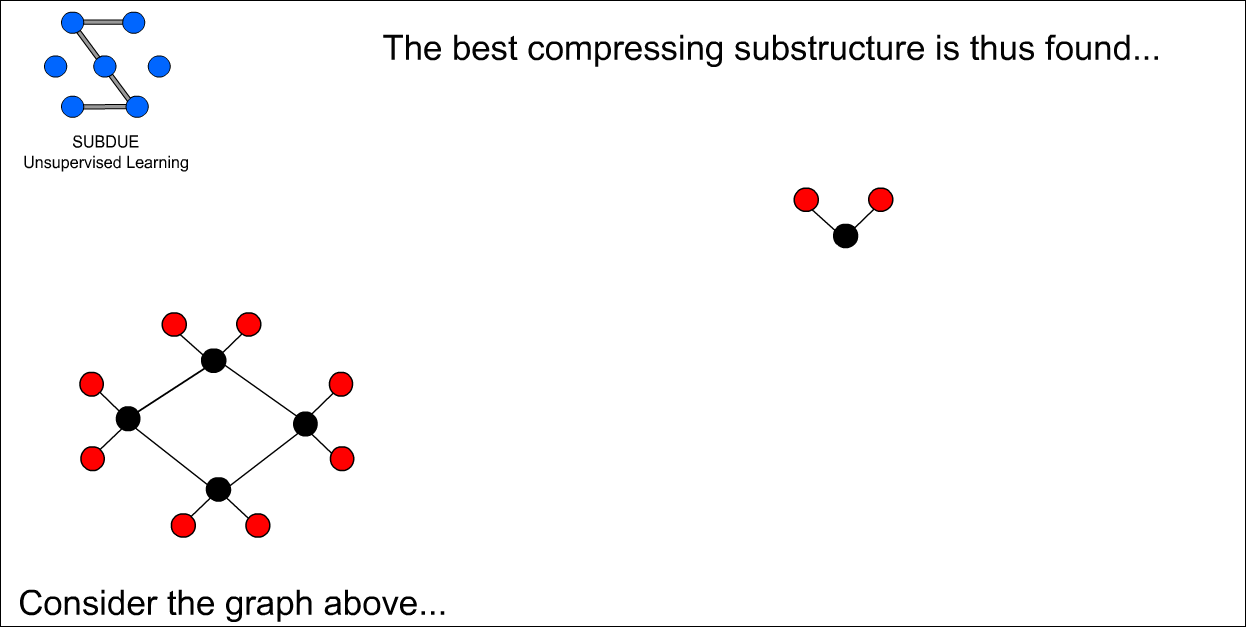
따라서 최종적으로 아래의 그래프 패턴이 best structure로 선정되었다. (강한 추측으로 더 확장을 시도해도 평가값인 아래의 구조가 제일 컸을것으로 본다.)