개요
컴파일러의 형식언어와 유한 오토마타에 대해 알아본다. 이 글은 내공 있는 프로그래머로 길러주는 컴파일러의 이해의 내용을 기반으로 함을 미리 밝힌다. 책 내용이 괜찮으니 관심있으신 분들은 사보는것을 추천한다.(필자는 이해관계자는 아님을 밝힌다.)
목차
컴파일러 강의 다른 포스팅은 아래의 링크를 참고하자.
- 컴파일러 강의 #1, 개요
- 컴파일러 강의 #2, 형식언어와 유한 오토마타
- 컴파일러 강의 #3, 컴파일러의 어휘분석
- 컴파일러 강의 #4, 문맥자유 문법과 푸시다운 오토마타
- 컴파일러 강의 #5, 컴파일러의 구문 분석
- 컴파일러 강의 #6, 의미 분석과 형 검사
- 컴파일러 강의 #7, 중간 언어와 중간 코드 생성
- 컴파일러 강의 #8, 코드 최적화
학습목표
- 형식언어를 이해
- 형식문법을 이해
- 문법의 표기법에 대한 이해
- 유한 오토마타에 대한 이해
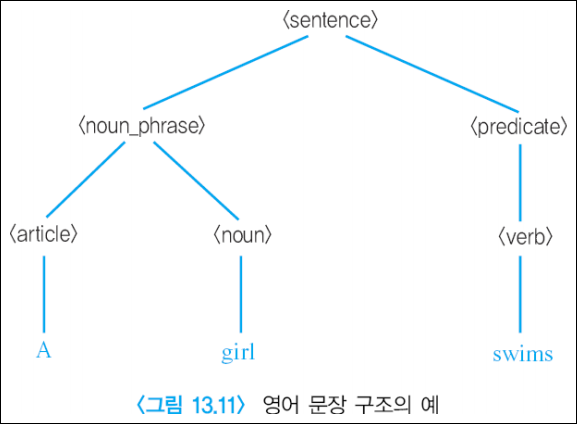
영어의 부분 집합
- 문법은 어떤 문장이 제대로 작성되었는지를 판단하는 기준

파스트리
형식언어: 기본 용어
-
알파벳
- 언어의 문장을 이루는 기본 기호(symbol)
- 알파벳이란 공집합이 아닌 기호들의 유한집합을 $ \sum$으로 표시
-
$ \sum_1 = $ {ㄱ, ㄴ, ㄷ, ㄹ, …, ㅎ}
$ \sum_2 = $ {a, b, c, … z}
$ \sum_3 = $ {0, 1} -
문자열
- 알파벳 $ \sum $에 대한 문자열은 알파벳어서 정의된 기호들을 나열한 유한 수열
- 알파벳 $ \sum = $ {a, b, c}일때 ccba는 문자열
- 문자열은 언어이론에서 문장이나 단어와 동의어
- 알파벳 기호들은 a, b, c, …을 사용하고 문자열은 u, v,w, …로 나타냄
문자열 연산
- 문자열의 길이
- 문자열을 이루는 기호의 갯수, |w|는 문자열 w의 길이
- $ w_1 = abc, w_2 = abab $ 일때
- |$w_1$| = 3, |$w_2$| = 4
- w = $a_1a_2a_3…a_k$ 일때 |w| = k
- 문자열의 접속
- 두개의 문자열을 연결하여 문자열을 만드는 연산
- 문자열 u, v가 각각 u = $a_1a_2a_3…a_n$, v=$b_1b_2b_3…b_m$일 경우 두 문자열의 접속은 $u \cdot v$ 또는 uv로 표시하고 uv = $_1a_2a_3…a_nb_1b_2b_3…b_m$이다.
- u=dog, v=house일때 $u \cdot v$ = doghouse, $v \cdot u$ = housedog이다.
공문자열
- 문자열의 길이가 0인 문자열
- $ \epsilon$으로 표시
- 어떤 문자열 u에 대해 다음과 같은 속성을 가짐
- $u\epsilon = u = \epsilon u$
- $\epsilon$은 접속 연산의 항등원
- $w^n$은 w가 n개 연결된 문자열 $w^0$은 공문자열
즉, $w^n=ww…w$(w가 n개)이고 $w^0 = \epsilon$이 됨
접두사, 접미사, $\sum^*$
- $\sum^*$
알파벳 $\sum$에 대해 접속 연산에 의해 만들어질 수 있는 모든 문자열의 집합 - $\sum^+ = \sum^* – \epsilon$
- $\sum = ${0,1}, $\sum^* = $ {$\epsilon$, 0, 1, 00, 01, 10, 11, 000, …}
- $\sum = ${a, b, c}, $\sum^* = $ {$\epsilon$, a, b, c, aa, bb, cc, ab, ba, ac, ca, bc, cb, aaa, …}
언어의 정의
- 언어 L
알파벳 $\sum$에 대한 언어 L은 $\sum^*$의 부분 집합- $\sum$ = {a, b}
- 아래 언어들의 숫자는 그냥 Naming이지 규칙이 있는것은 아님
- $L_1 $ = $\sum^* = $ {$\epsilon$, a, b, c, aa, bb, cc, ab, ba, ac, ca, bc, cb, aaa, …}는 무한 언어
- $ L_2 $ = {a, ba, bbb}는 유한언어
- $ L_3 $ = {aaa, bbb, ccc}는 유한언어
- $ L_4 $ = {$a^p$|p는 소수}는 무한언어
- $ L_5 $ = {$a^nb^n$|n >= 1}는 무한언어
- 여기서 언어는 의미 개념은 포함하지 않음
언어에서의 연산
- 아래 문법으로 생성되는 언어
- G = ({S,A}, {b, d}, P, S)
- P : S -> dAd
- A -> dAd
- A -> b

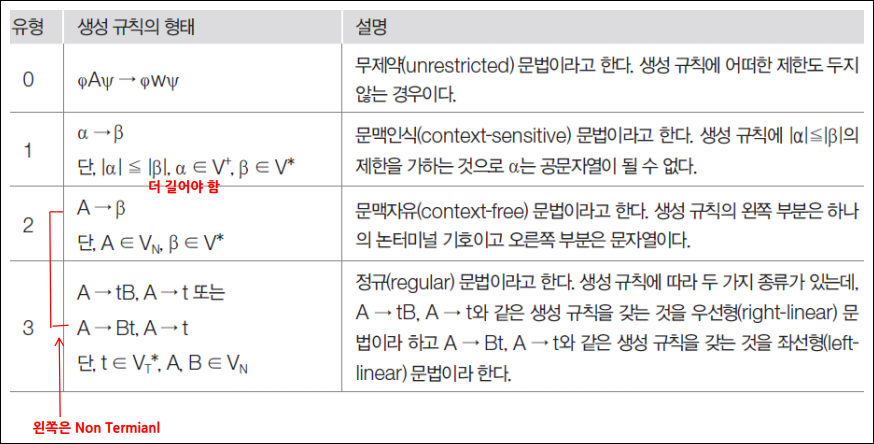
촘스키 계층 구조
- 문법을 생성 규칙에 가해지는 제한에 따라 네종류로 나누었으며 이를 촘스키 계층 구조라고 부름
문법의 표기법
- 정규표현
- 문법도표
- BNF
- EBNF
문법의 표기법: 정규표현
- 정규표현 : 정규언어를 표현할 수 있는 한 방법
- 다음과 같이 재귀적으로 정의
- 기본단계
- $ \phi $는 공집합을 나타내는 정규표현
- $\epsilon$은 집합 {$\epsilon$}를 나타내는 정규표현
- 터미널 기호 a 는 집합 {a}를 나타내는 정규표현
- 귀납단계 : 만일 r, s가 정규언어 $L_r$, $L_s$를 표현하는 정규표현이라하면
- r + s 는 $L_r \cup L_s$
- $r \cdot s$는 $L_r \cdot L_s$를 나타내는 정규표현
- $r^$는 $L_r^$를 나타내는 정규표현
- 연산자 우선순위는 * > $\cdot$ > +이다.
정규 표현의 연산 순서
- 다음 정규 표현의 연산 순서는?
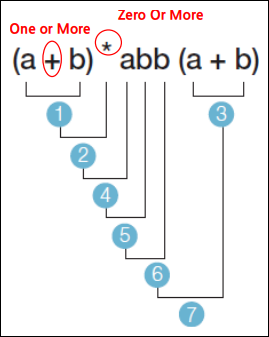
정규표현에 의해 생성되는 언어의 예

- 한문제 더

정규표현인지 판단의 예


Syntax diagram(문법도표)
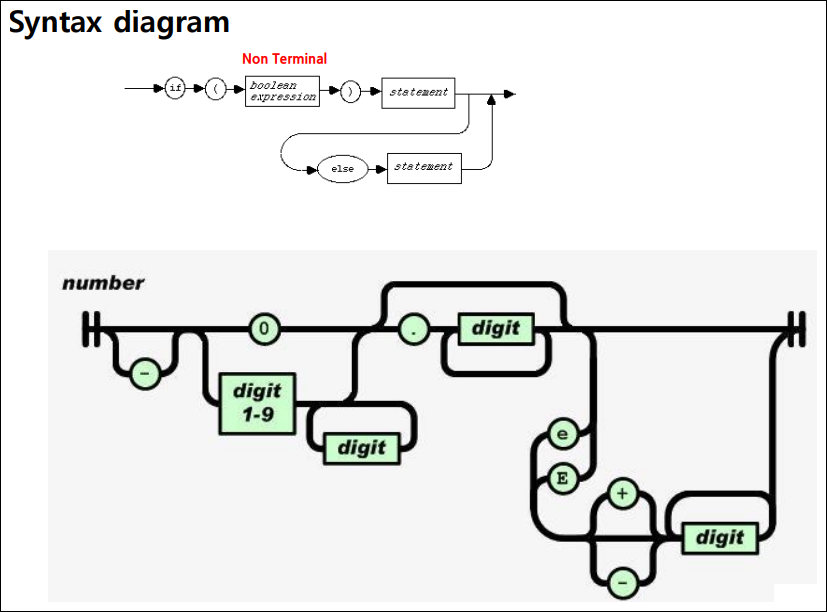
문법의 표기법: 문법 도표
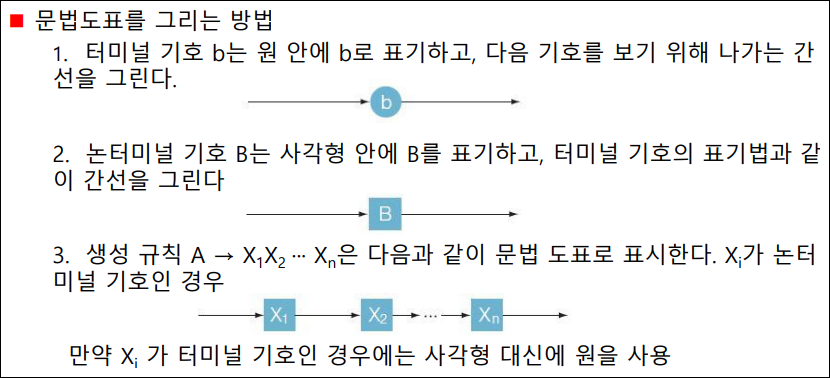
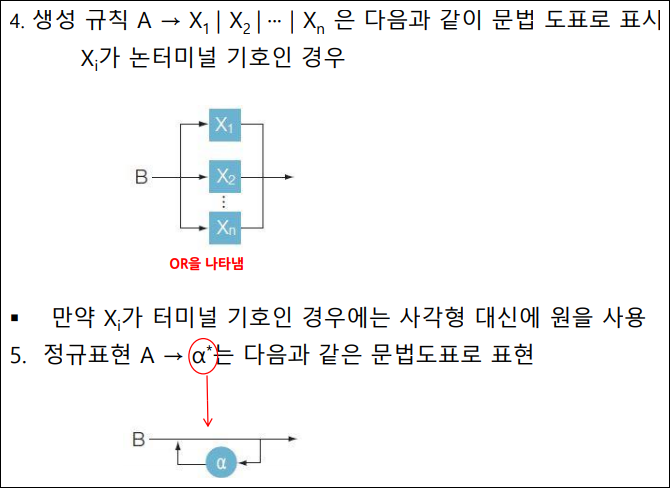
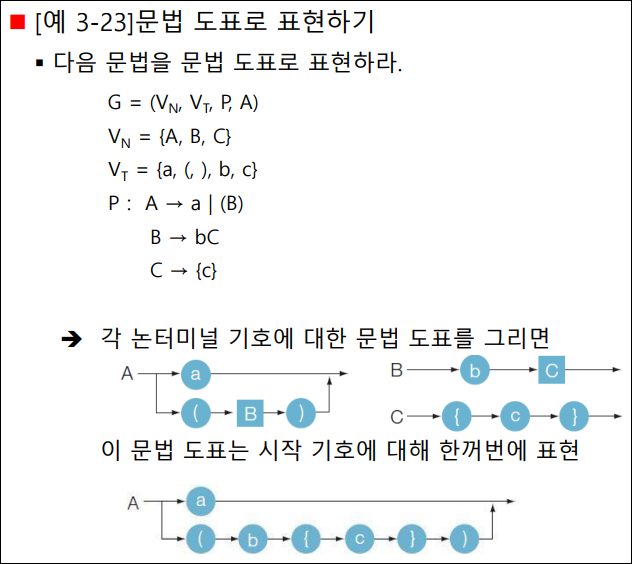
- 문법 도표
- 쉽게 이해할수 있도록 문법을 도식화 하는 방법
- 문법도표는 사각형과 타원, 간선으로 구성
문법의 표기법: BNF(Backus-Naur Form) 표기법
- BNF 표기법
- 프로그래밍 언어의 형식적 정의를 위해 가장 널리 사용하는 방법
- 현재 대부분 언어들을 표현하는데 많이 사용
- 메타기호로 3가지 기호를 사용
- 논터미널은 < 와 > 를 묶어 표현
- 대체를 위해 ::= 를 사용
- 양자 택일을 위해 |를 사용
BNF로 표현의 예

BNF의 문제점

문법의 표기법: EBNF(Extended BNF) 표기법
- EBNF 표기법
- 반복되는 부분을 BNF 표기법보다 가독성있게 표현
- 반복을 나타내는 기호로 {} 와 [] 를 사용
- {a}는 0번 이상 반복을 의미
- 선택적인 부분을 표시할때는 [] 를 표현
- [x]는 x가 나타나지 않거나 한번 나타남을 의미
EBNF로 표현의 예

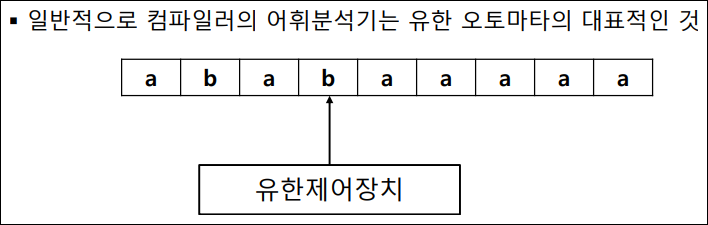
유한 오토마타
- 어휘분석기의 출력인 토큰은 정규표현으로 표현
- 유한 호토마타를 자동 또는 수동으로 만들면 어휘분석기가 된다
- 유한 오토마타
알파벳 $\sum$으로부터 만들어지는 문자열의 특별한것들을 받아들이는 시스템의 수학적모델로서 그 시스템에서 변화할 수 있는 상태가 유한개일것
유한 오토마타: 상태 전이도
- 상태전이도
- 각 상태를 노드로 표현
- 간선은 전이
- 전이 함수 $\delta(q,a) =p $에 대해서는 상태 q에서 p로 가는 라벨이 a인 간선으로 표기
- 최종 상태는 이중원(double circle)로 표기, 시작상태는 directed graph로 표현
예제는 아래와 같다.
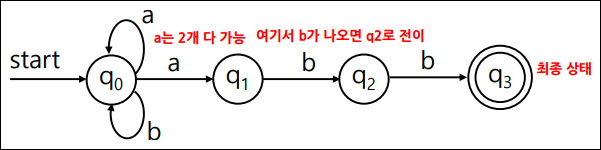
- 시작상태 q0에서 a를 받력받으면 q0를 유지하거나 q1으로 상태 전이
- q1 상태에서 b를 입력받으면 q2로 전이
- q2에서 b를 입력받으면 q3로 전이
- q3는 최종 상태
유한 오토마타: 상태전이도로 표현의 예
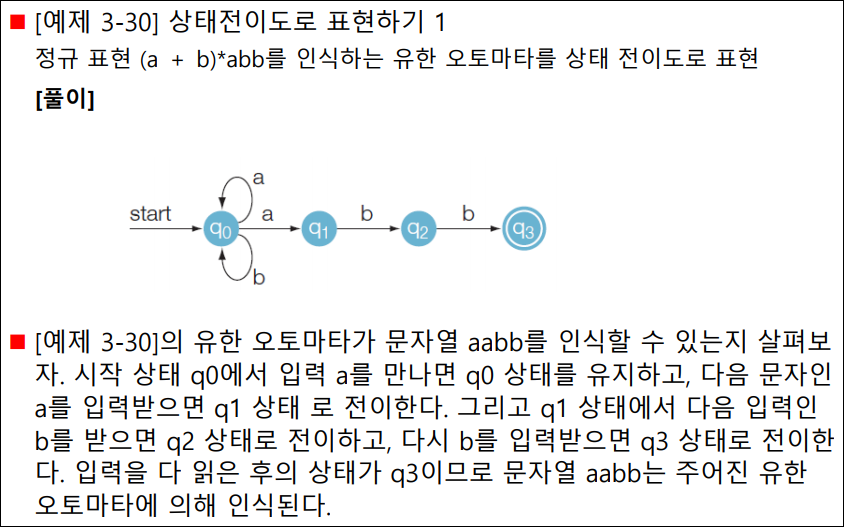
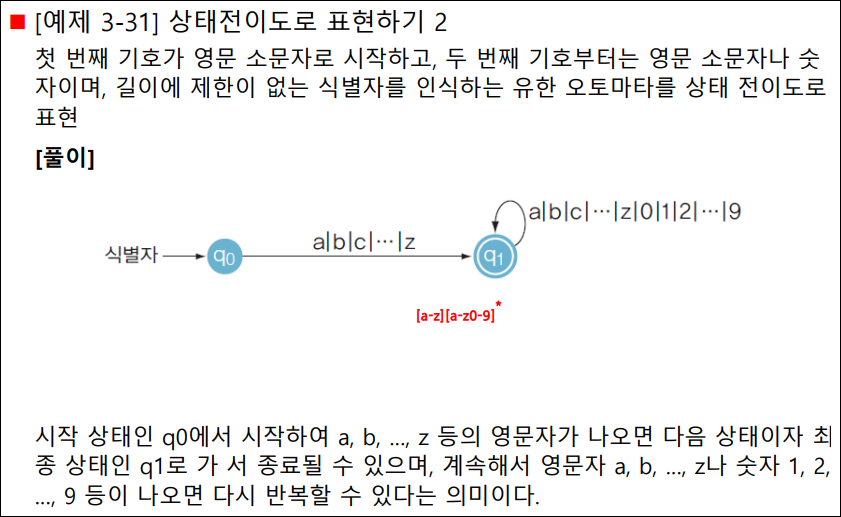
유한 오토마타의 정의
- 정의
유한 오토마타를 M이라 하면 M = (Q,$\sum$, $\delta$,$q_0$, F)- Q : 상태들의 유한 집합
- $\sum$ : 입력 기호들의 유한 집합
- $\delta$ : 전이함수
- $q_0$ : 시작 상태, $q_0 \in$ Q
- F : 최종상태 F $\in$ Q
유한 오토마타: 정의의 예

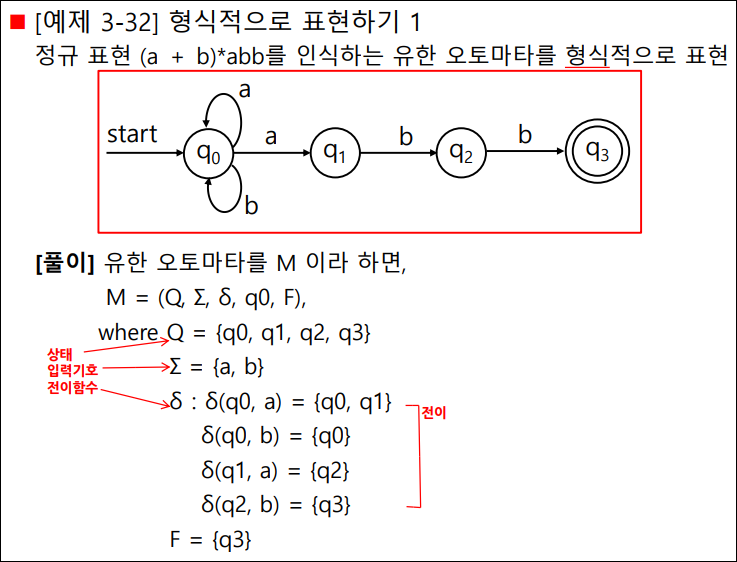
유한 오토마타: 전이표(state transition table)
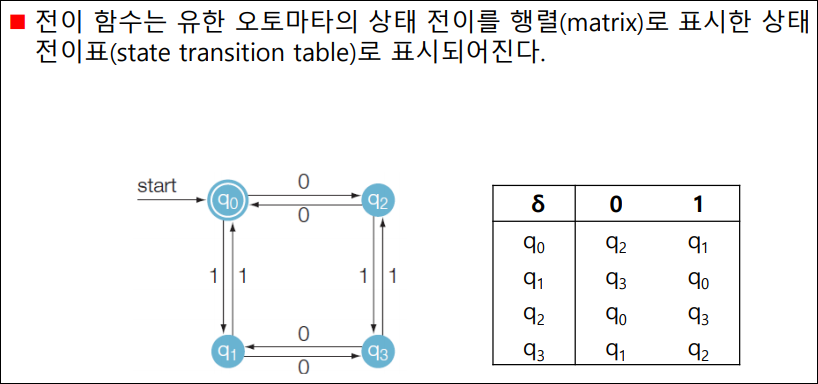
유한 오토마타: DFA 및 NFA 정의
- 상태 전이함수에 따라 아래로 분류
- DFA : 결정적 유한 오토마타
- NFA : 비결정적 유한 오토마타
- DFA
- 2가지 조건이 만족해야함
- $\epsilon$에 의한 상태전이가 없음
- 하나의 입력기호에 대한 다음 상태는 오직 하나
$\delta(q,a)$ = {$P_1$,$P_2$,$P_n$}에서 n = 1
- NFA
- $\epsilon$에 의한 상태전이가 있음
- 하나의 입력기호에 대한 다음 상태는 2개 이상인 경우가 있음
유한 오토마타: DFA의 상태전이도 표현
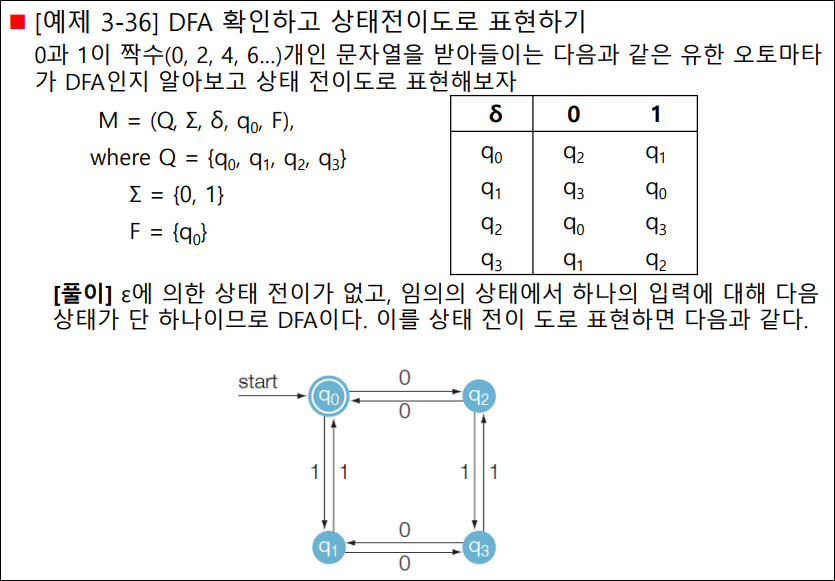
유한 오토마타: DFA로 부터 문장 인식하기
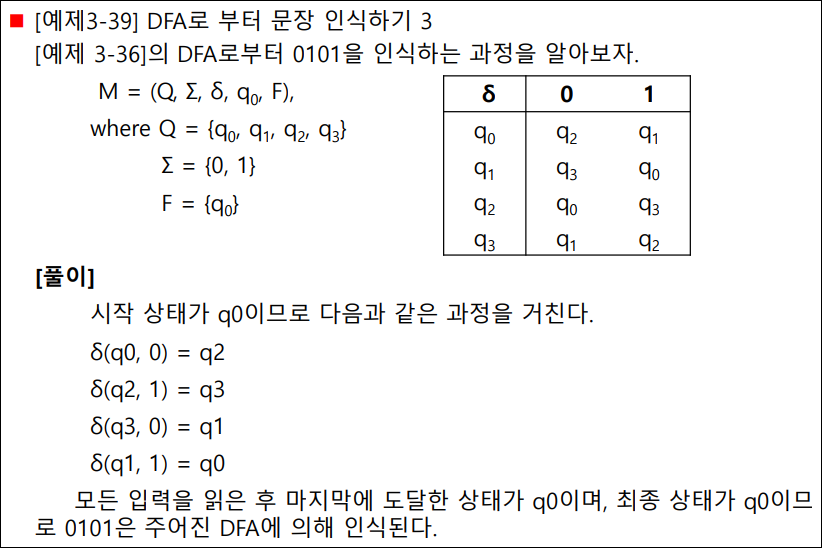
유한 오토마타: NFA인지 확인하고 상태전이도로 표현
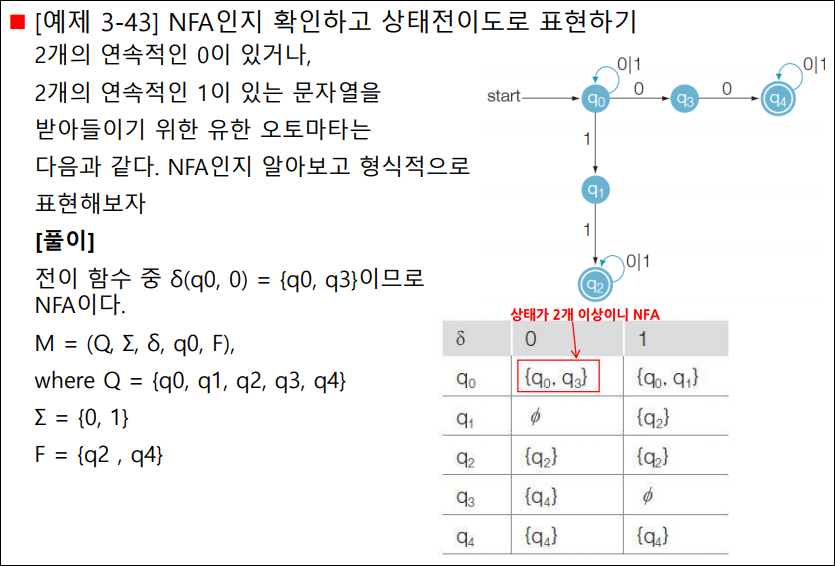
유한 오토마타: NFA의 문장 인식 여부

유한 오토마타
- NFA와 DFA
- NFA가 언어의 구조를 더 쉽게 표현
- NFA는 DFA보다 구현이 어려움
- DFA는 NFA보다 구현 효율성이 우수
- 여기서 생각할 수 있는 전략은 DFA와 NFA간 변환이 가능케 해서 DFA 프로그램을 활용하는 방법
- 어휘 분석기
- 토큰화 및 토큰들을 정규표현으로 표현
- 정규표현을 인식하는 NFA를 구성, NFA->DFA 변환, DFA의 상태를 최소화 하여 어휘분석기 생성
- 어휘분석기를 자동으로 생성하는 툴이 있음, 정규표현으로 입력
유한 오토마타: 정규 표현에서 유한 오토마타로 변환
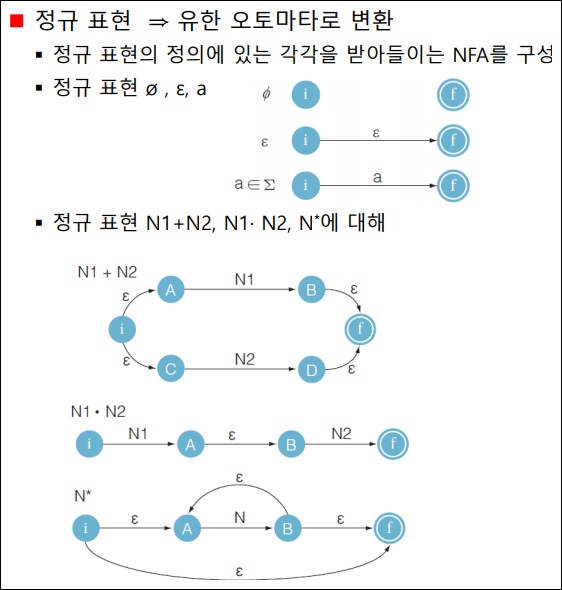
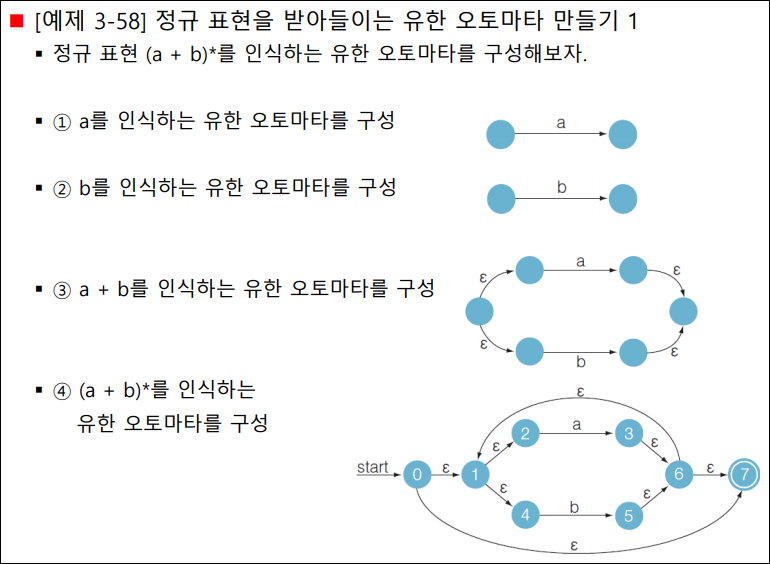
유한 오토마타: 정규 표현에서 유한 오토마타 만들기

요약
- 형식언어
- 형식 언어 L은 알파벳 $\sum$에 대해 $\sum^*$의 부분집합
- 형식문법
형식 문법 G = ($V_N$, $V_T$, P, S)는 다음과 같이 네 가지 항목으로 정의- $V_N$ : 논터미널 기호의 유한 집합
- $V_T$ : 터미널 기호의 유한 집합
$V_N \cap V_T$ = $\Phi$, $V_N \cup V_T$ = V - p : 생성 규칙의 유한 집합
$ \alpha \rightarrow \beta $, $\alpha \in V^+$, $\beta \in V^*$ - S:$V_N$에 속하는 기호로서 시작기호 라고한다.
- 문법표기법
- 정규표현 : 정규 언어를 가장 잘 표현할수 있는 방법
- 문법 도표 : 초보자가 쉽게 이해할수 있도록 문법을 도식화하는 방법
- BNF 표기법 : 프로그래밍 언어의 형식적 정의를위해 가장 널리 시용되는 방법
- EBNF 표기법 : 반복되는 부분을 BNF 표기법보다 읽기 쉽고 간결하게 표현하는 방법
- 유한오토마타
- 유한오토마타: 형식 언어를 인식하는 시스템의 수학적 모델로 그 시스템에서 변화할수 있는상태가 유한개인것
- 상태 전이도: 유한 오토마타의 각 상태를 노드로 표현하고, 간선은 전이를 나타낸다. 또한 최종 상태는 노드를 이중 원으로 나타내고 시작 상태는 시작 간선으로 표시하는 유향 그래프이다. 전이 함수 $\delta$(q, a) = p는 상태 q에서 입력 a를 받아상태 p로 전이할 때 노드 q에서 노드 p로 가는라벨이 a인 간선으로 나타냄
- DFA :첫째. $\epsilon$에의한상태 전이가 없고, 둘째,$\delta$(q, a) = {$p_1$, $p_2$, …,$p_n$}에서
n = 1, 즉 5 :QxS $\rightarrow$ Q - NFA :첫째. $\epsilon$에 의한상태 전이가 있거나,둘째, $\delta$(q, a) = {$p_1$, $p_2$, …,$p_n$}에서
n>=2인 n이 하나라도 존재, 즉 $\delta$ : Q x S $\rightarrow$ $2^Q$