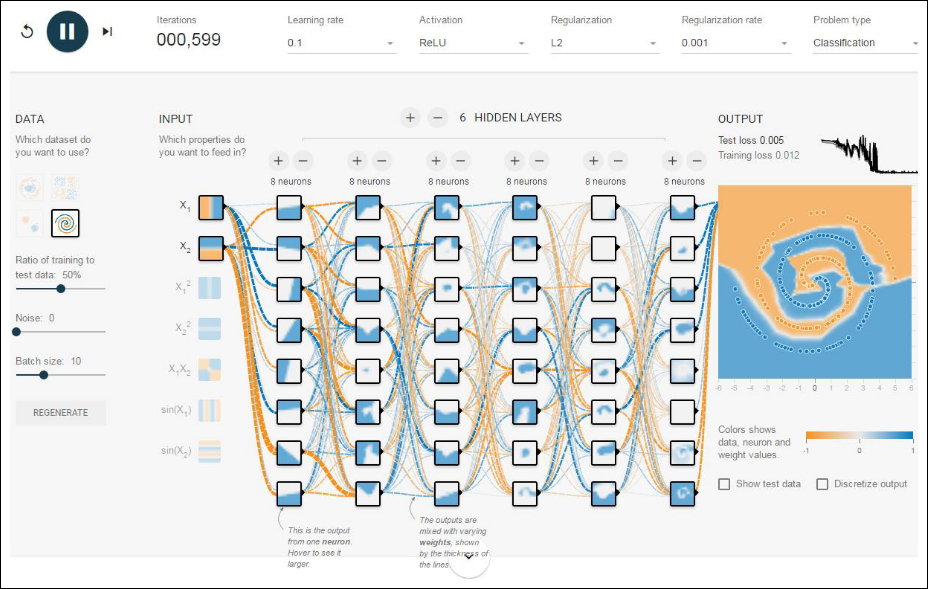
Slide
SlideShare에 올려놓은 슬라이드 버전은 아래와 같습니다.
Content
- Multilayer Perceptron (MLP) (Commonly known as neural network by lay person)
- Error Function (Loss Function) of MLP
Multilayer Perceptron (1/2)
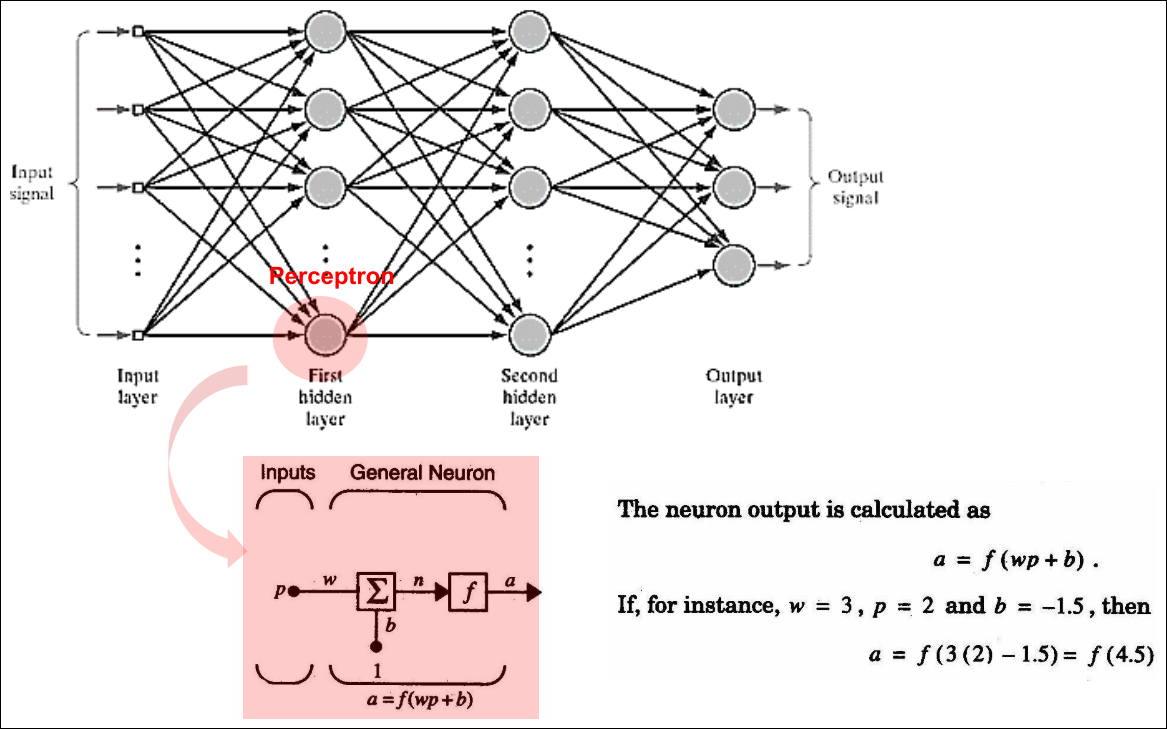
Multilayer Perceptron (2/2)
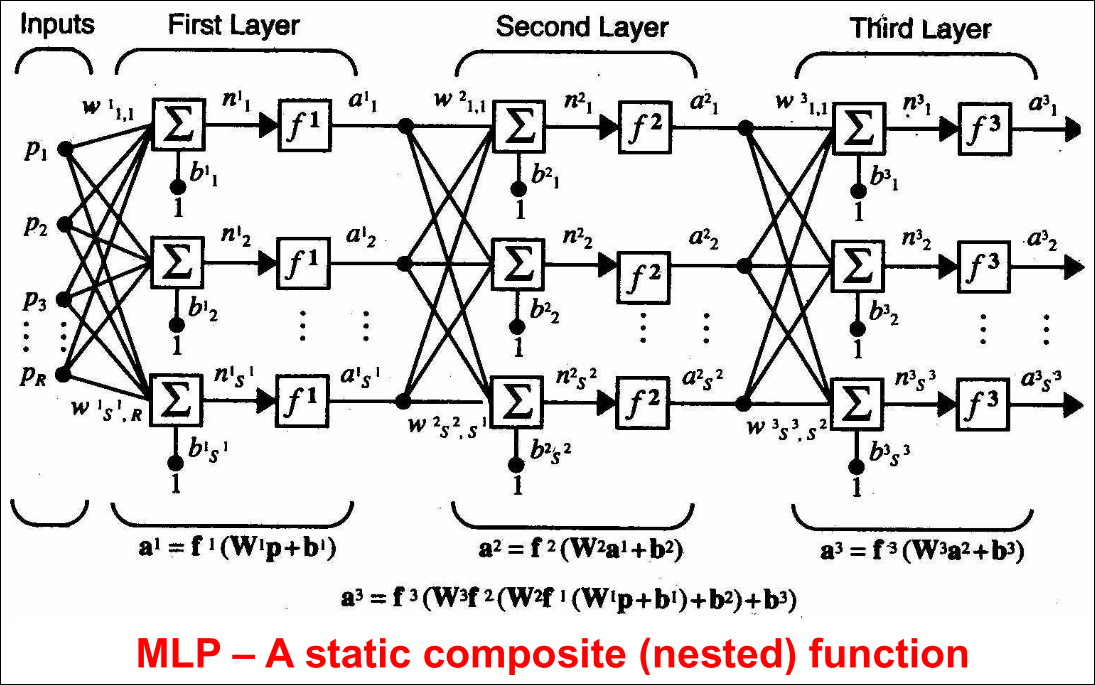
Multiple Layer Perceptron (MLP)
-
MLP는 fully connected임
-
MLP는 classification, regression 모두에 쓰일 수 있음
MLP Architectures (1/2)
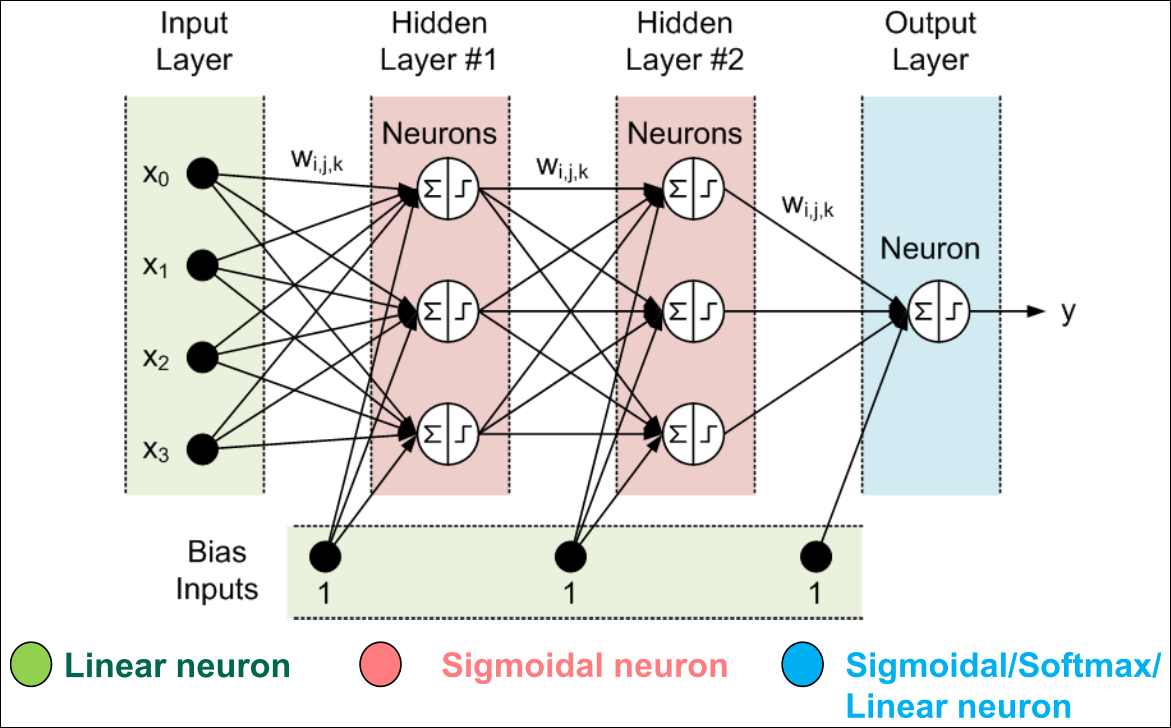
MLP Architectures (2/2)
- 히든 레이어의 활성화 함수로 전통적으로 sigmoid를 사용
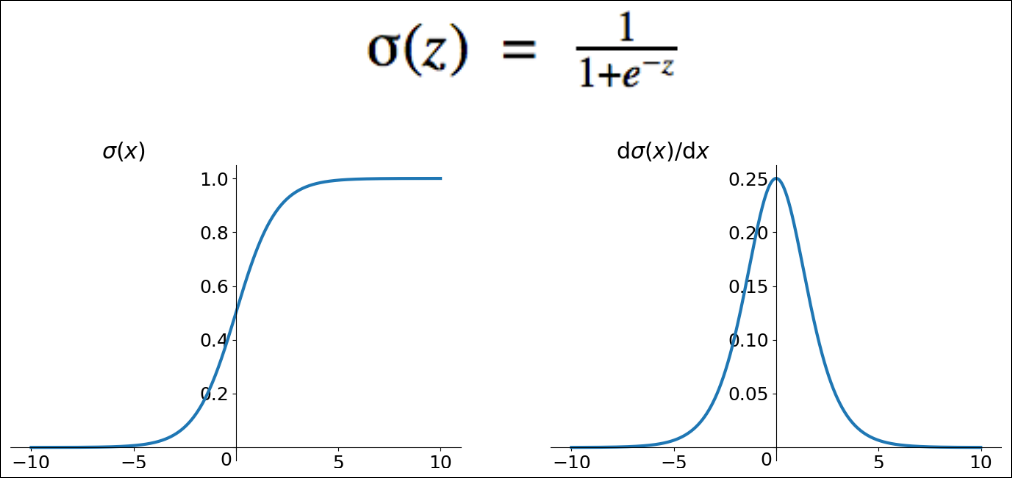
- 왜 step function을 사용하지 않는가? 미분을 가능케 하기 위해
Other Commonly use Activation Functions
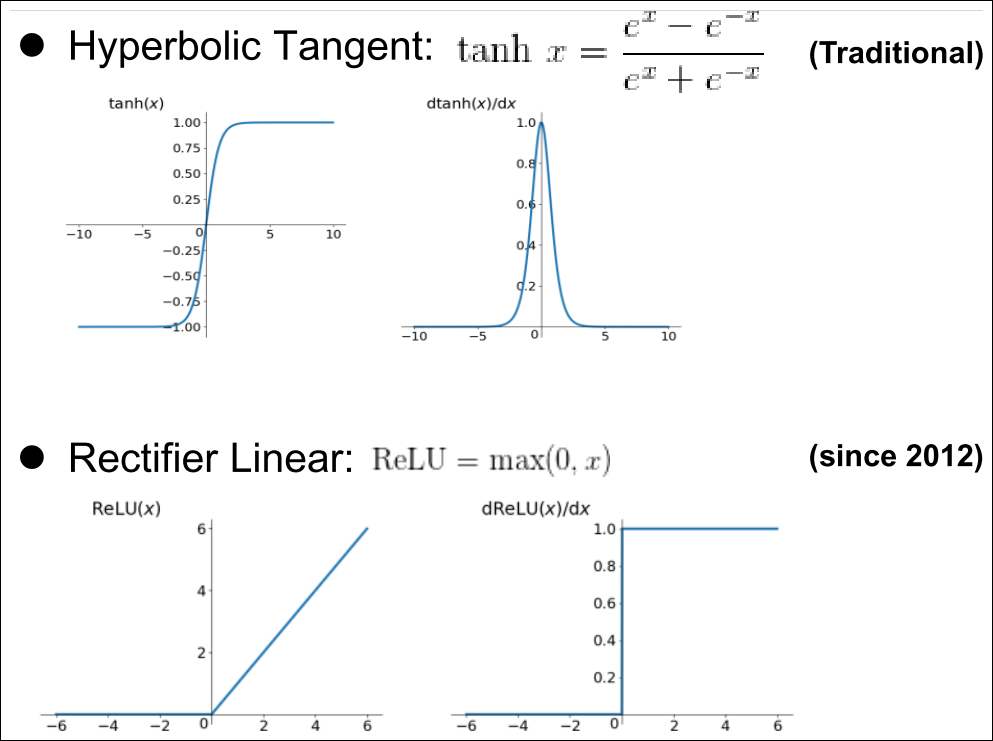
MLP Architectures
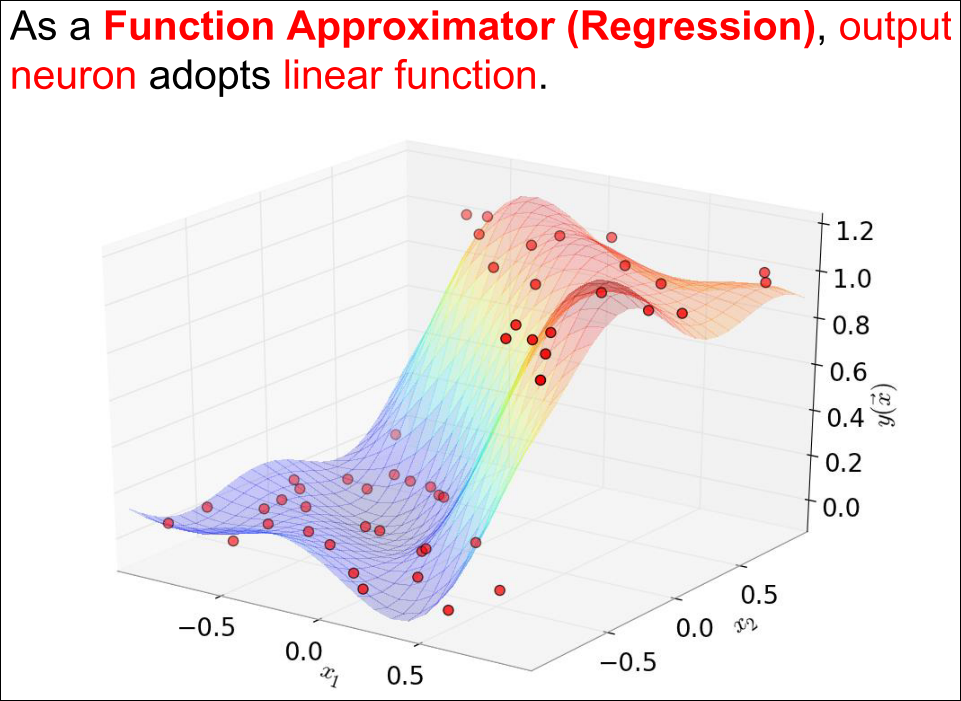
- Classification 문제에서 출력 뉴런은 아래와 같이 구성 가능

Example
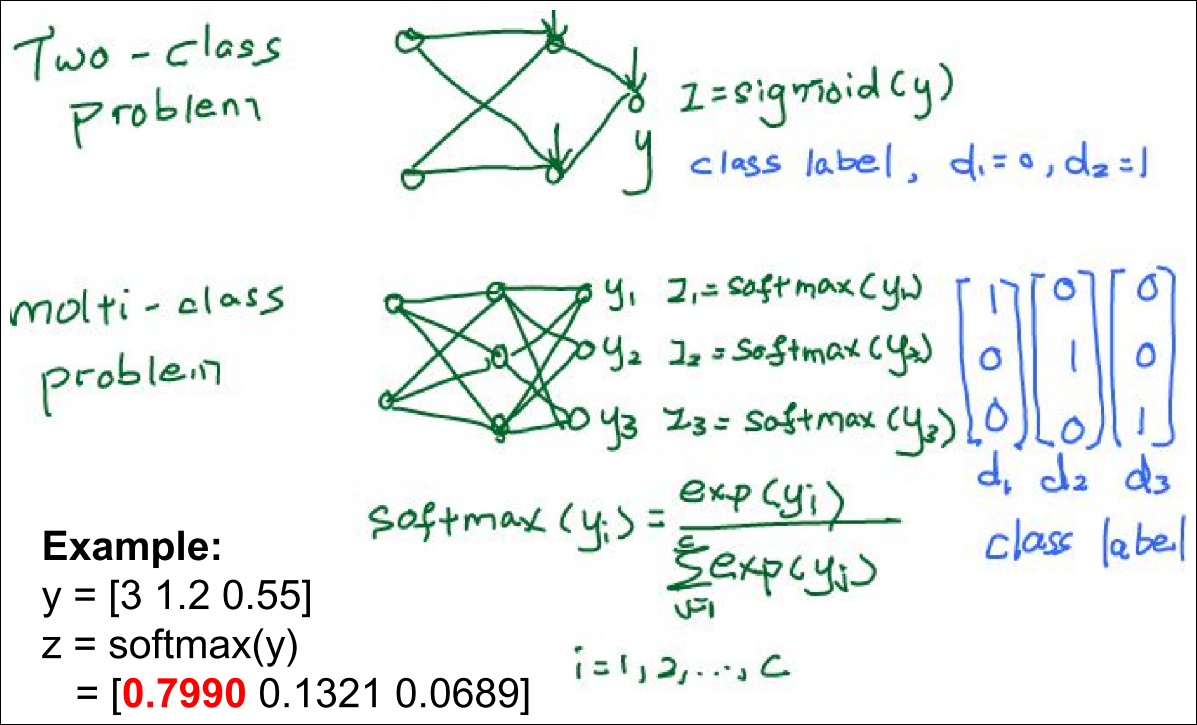
Multiple Layer Perceptron (MLP)
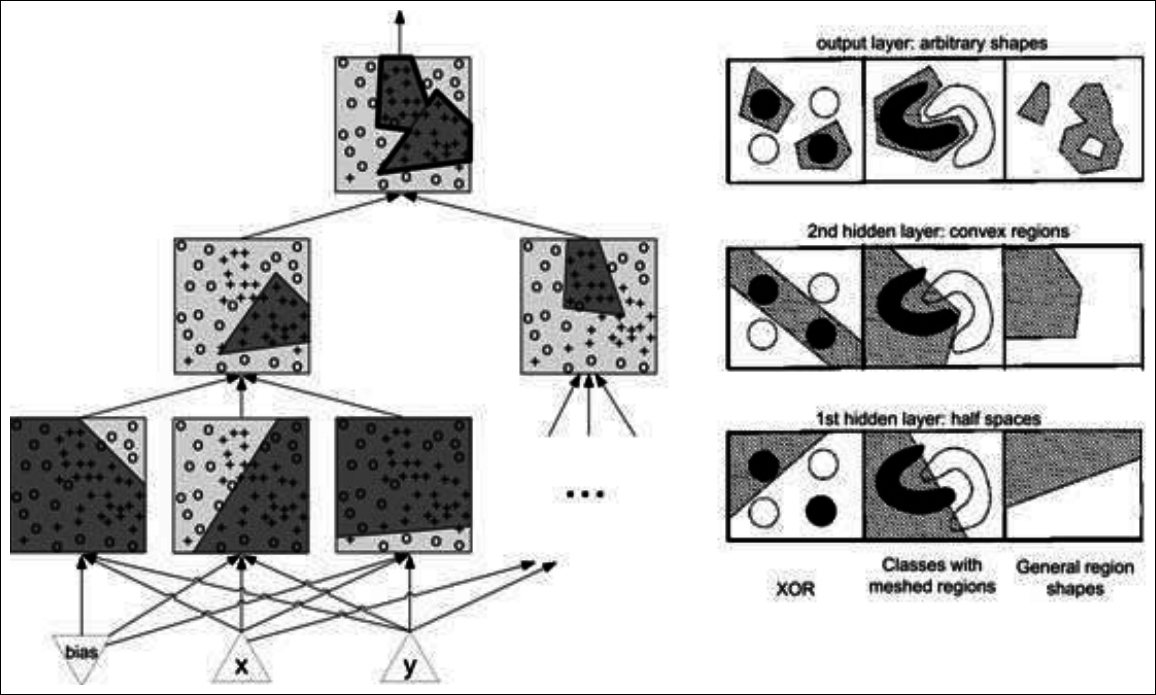
Illustration
Multiple Layer Perceptron (MLP)
Multiple Layer Perceptron (MLP)
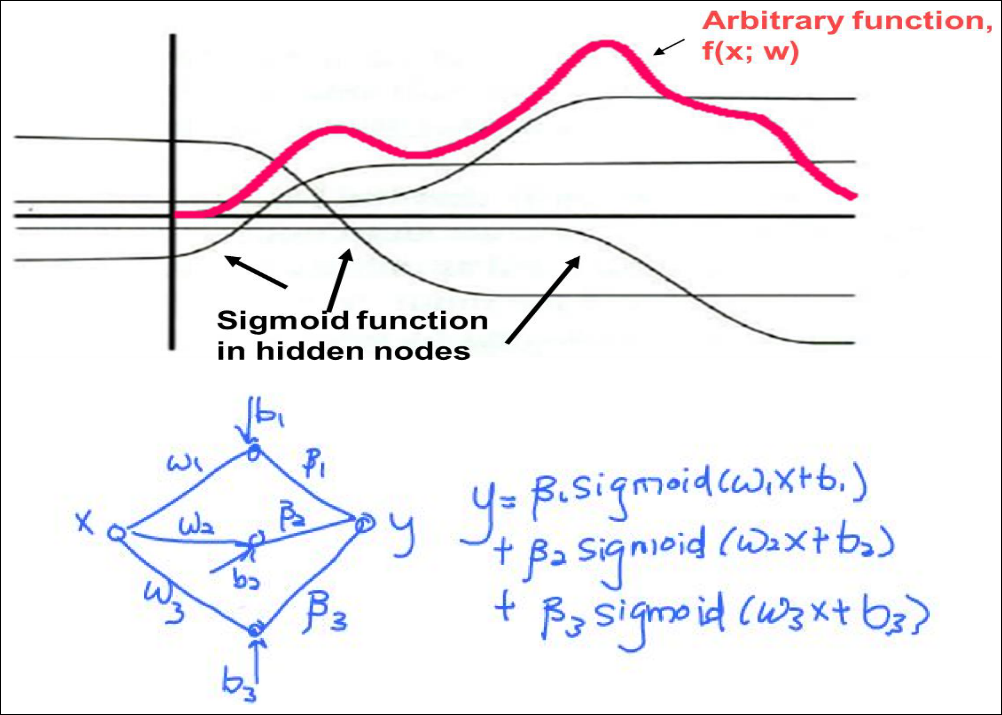
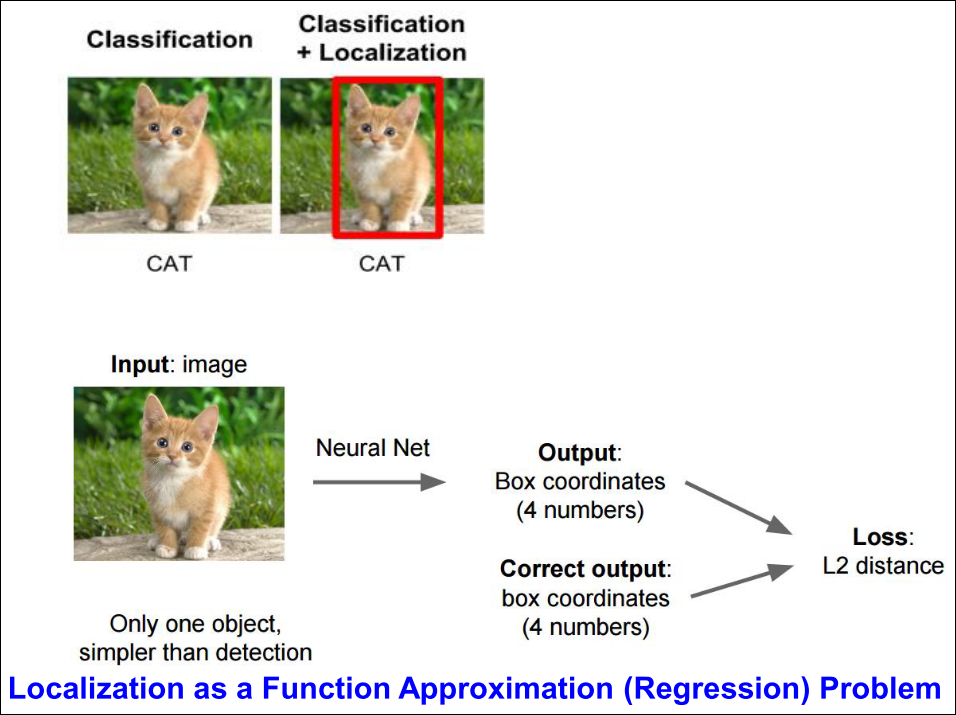
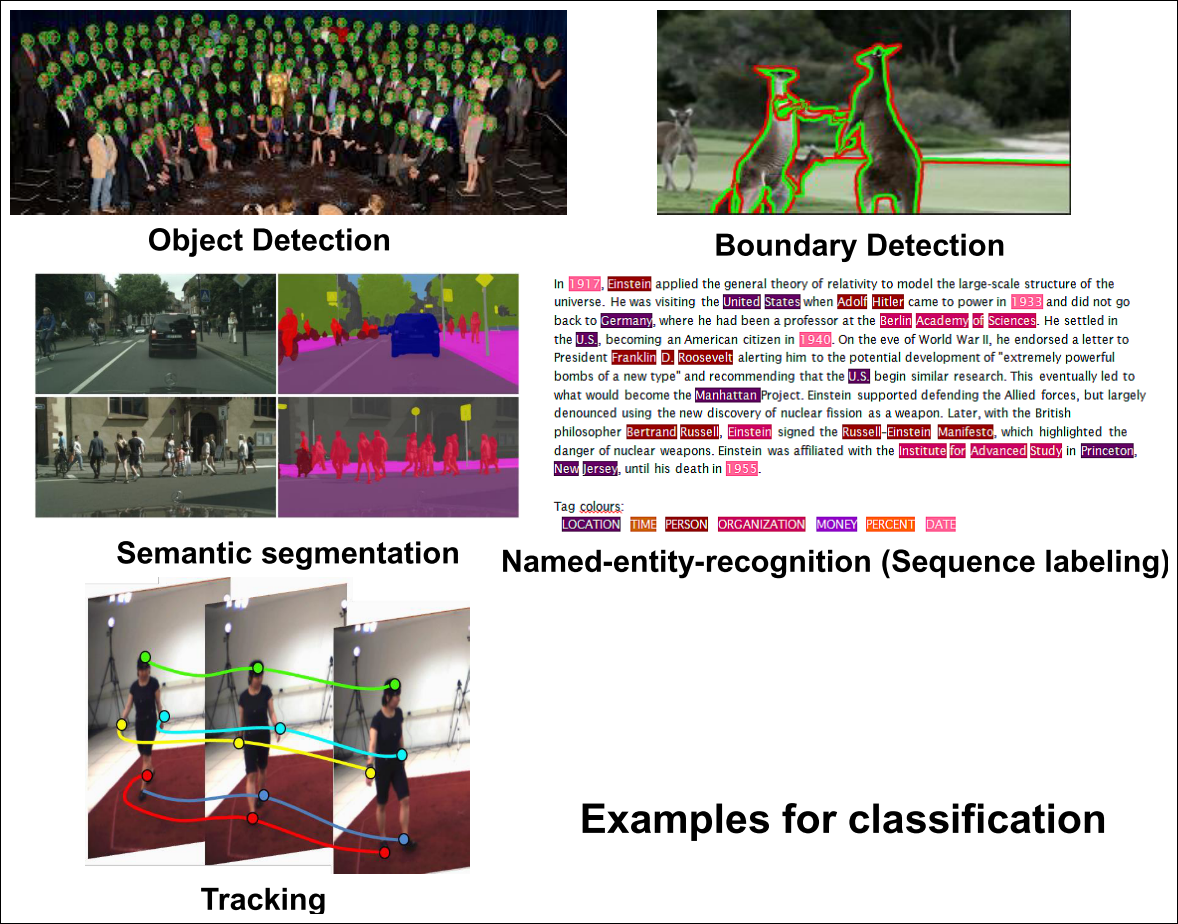
Common Error/Loss Functions used in MLP
Recall
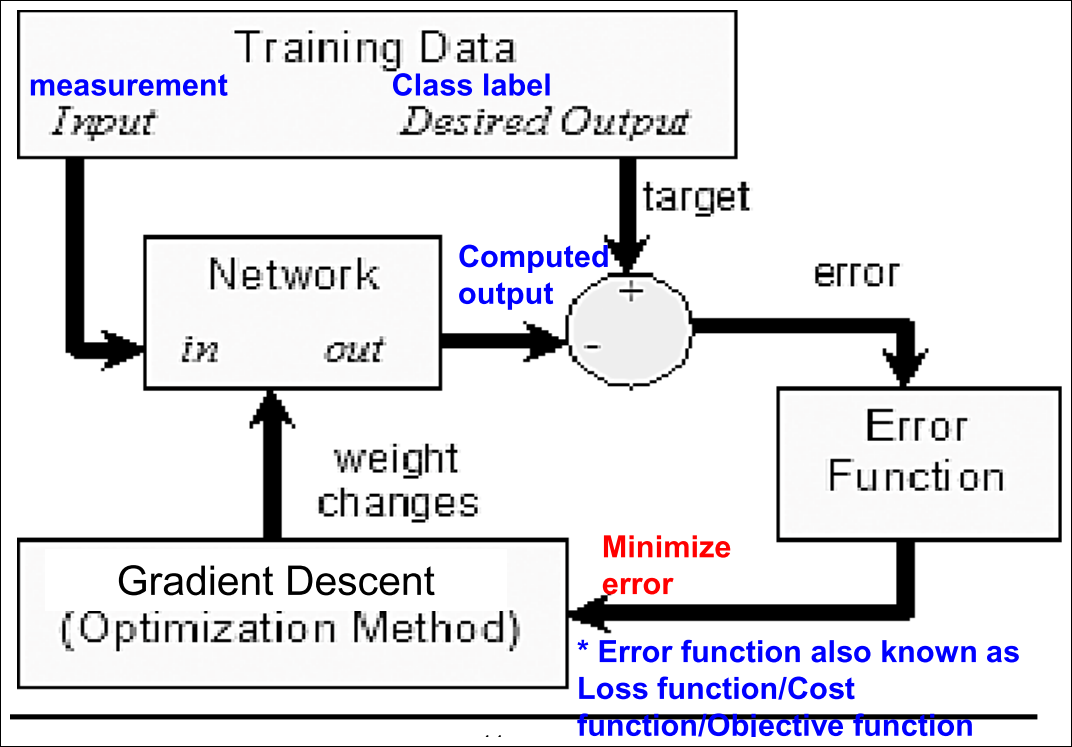
Mean Square Error (MSE) for Regression
- MSE Loss
$$ \epsilon_k = \frac {1}{2} \sum_{j=2}^p (d_j^k – S(y_j^k))^2 $$
$$ \epsilon = \frac {1}{Q} \sum_{k=1}^Q \epsilon_k$$
- Q = # of training data
Error Function in the Weight Space
- Error function epsilon(w)는 못생김
- 매우 높은 차원
- non-linear
- global minima는 도달 불가능할 수 있음
- local minima는 bad or good
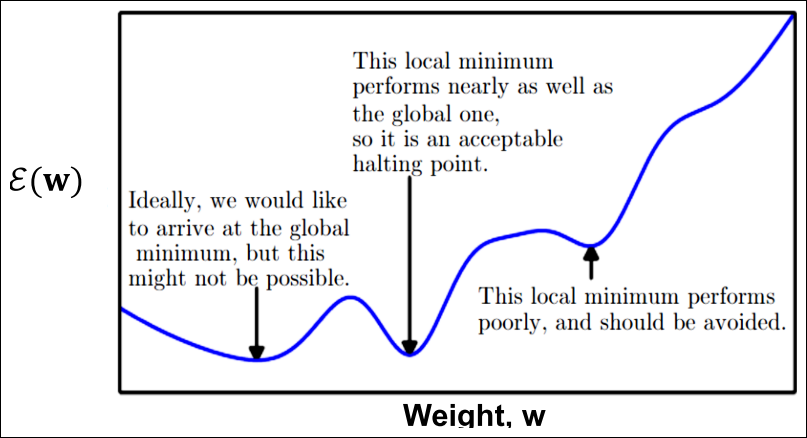
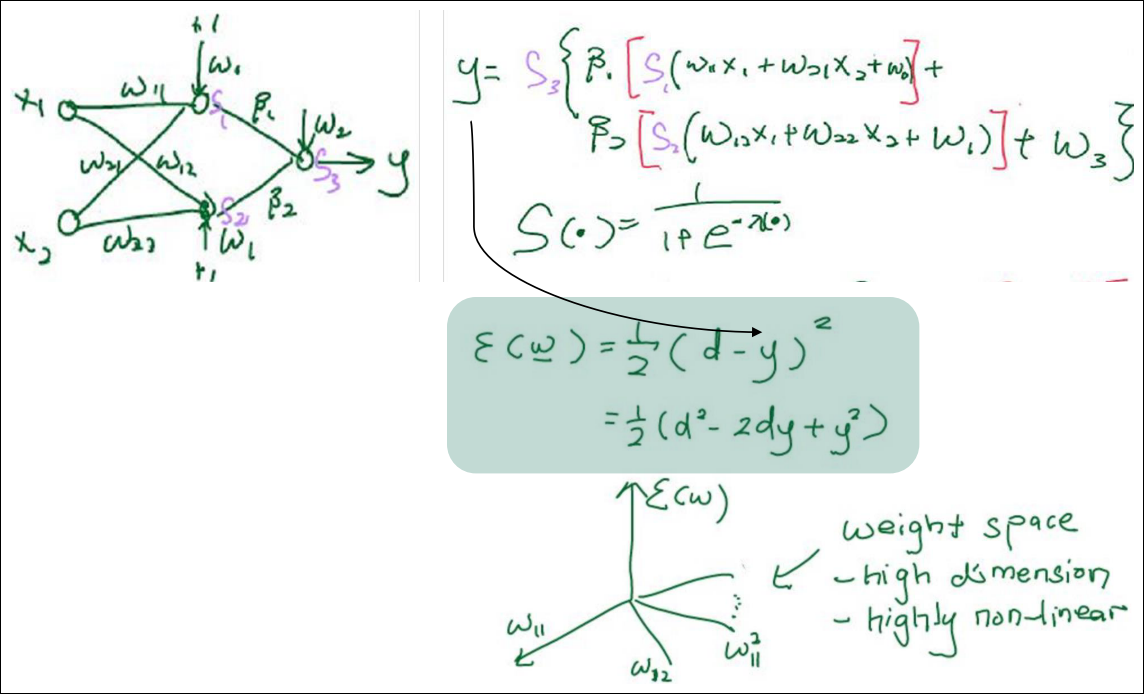
Ugly Error Function

Cross-Entropy for Classification


Error Functions
-
에러 함수는 validation/test 셋에서는 사용하지 않음
-
에러 함수는 학습 단계에서의 이정표 역할을 해줌 -> 에러를 줄여 최적의 가중치를 찾기위해
다음강의
-
GD 알고리즘을 배웠는데 하나의 단일 뉴런의 가중치 최적화를 알아보자.
-
GD를 MLP에는 어떻게 적용할 수 있을까?
Quiz 3

Assumption
If we assume $f^1, f^2, f^3$ is linear function. We can say a^1 = f^1(w^1p+b^1) becomes also linear function since (w^1p+b^1) is a linear function. after applying $f^1$, each data points just move within linear space.
Proof
Let’s replace f^1, f^2, f^3 = p which means it’s a identity function and to make calculation simpler.
$$ a^3 = f^3(w^3f^2(w^2f^1(w^1p+b^1)+b^2)+b^3) $$
$$ a^3 = f^3(w^3f^2(w^2(w^1p+b^1)+b^2)+b^3) \ since \ f^1 = p$$
$$ a^3 = f^3(w^3f^2(w^2w^1p+w^2b^1+b^2)+b^3) $$
$$ a^3 = f^3(w^3(w^2w^1p+w^2b^1+b^2)+b^3) \ since \ f^2 = p$$
$$ a^3 = f^3(w^3w^2w^1p+w^3w^2b^1+w^3b^2+b^3) $$
$$ a^3 = w^3w^2w^1p+w^3w^2b^1+w^3b^2+b^3 \ since \ f^3 = p$$
$$ a^3 = w^3w^2w^1p+w^3w^2b^1+w^3b^2+b^3 $$
we can say
$$ a^3 = Ap+C \ where \ A = w^3w^2w^1, C = w^3w^2b^1+w^3b^2+b^3 $$
As a result, final activation function a ^ 3 is a single linear neuron.
This only makes 1-dimension decision boundary(hyperplane), so it can’t solve complex classification problem(using more than 2-dimension hyper plane).
So, we should use non-linear activation function in MLP.