개요
컴파일러의 문맥자유 문법과 푸시다운 오토마타에 대해 알아본다. 이 글은 내공 있는 프로그래머로 길러주는 컴파일러의 이해의 내용을 기반으로 함을 미리 밝힌다. 책 내용이 괜찮으니 관심있으신 분들은 사보는것을 추천한다.(필자는 이해관계자는 아님을 밝힌다.)
목차
컴파일러 강의 다른 포스팅은 아래의 링크를 참고하자.
- 컴파일러 강의 #1, 개요
- 컴파일러 강의 #2, 형식언어와 유한 오토마타
- 컴파일러 강의 #3, 컴파일러의 어휘분석
- 컴파일러 강의 #4, 문맥자유 문법과 푸시다운 오토마타
- 컴파일러 강의 #5, 컴파일러의 구문 분석
- 컴파일러 강의 #6, 의미 분석과 형 검사
- 컴파일러 강의 #7, 중간 언어와 중간 코드 생성
- 컴파일러 강의 #8, 코드 최적화
문맥 자유문법(Context-free grammar)
- 잘 설계된 문법은 소스 프로그램을 정확한 목적코드로 번역할 때 유용한 구조를 제공
- 문법자유 문법은 프로그래밍 언어설계 뿐만 아니라 효율적인 컴파일러 작성시에도 중요하게 사용
- 문법 정의, $ G=(V_N, V_T, P,S) $
- $V_N$ : 논 터미널 기호들의 유한 집합
- $V_P$ : 터미널 기호들의 유한 집합
$V_N \cap V_T = \Phi, V_N \cup V_T = V $ - P : 생성규칙의 집합
$ \alpha \rightarrow \beta, \alpha \in V^+, \beta \in V^* $ - S : $V_N$에 속하는 기호로서 다른 논터미널 기호들과 구별되는 시작기호
- 모든 생성규칙이 $ A \rightarrow \beta$ 형태일때 문맥자유문법. 단 $ A \in V_N, \beta \in V^* $
- A가 $\beta$로 치환 : A는 $\beta$로 유도, A는 $\beta$를 생성
- $\beta$가 A로 치환 : $\beta$는 A로 reduce
정의: leftmost derivation, rightmost derivation
- 좌단 유도는 유도과정의 각 단계에서 가장 왼쪽에 있는 논터미널 기호를 계속 대체하는 경우
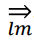 으로 표시
으로 표시 - 우단 유도는 유도 과정의 각 단계에서 가장 오른쪽에 있는 논터미널 기호를 계속해서 대체하는 경우
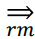 로 표시
로 표시

좌파스, 우파스
- 좌파스, 우파스
- 좌파스 : 좌단 유도에 의해 적용된 생성규칙 순서
- 우파스 : 우단 유도에 의해 적용된 생성규칙 순서의 역순

파스 트리(parse tree) 의 정의
- 구문 분석 방법은 크게 두 종류가 존재
- 하향식(top-down) 구문분석
좌파스를 생성 - 상향식(bottom-up) 구문분석
우파스를 생성
- 하향식(top-down) 구문분석
- 파스트리는 루트노드, 중간노드, 리프노드로 구성
- 루트노드 : 정의된 문법의 시작기호
- 중간노드 : 각 생성규측의 좌측 논터미널 기호
- 리프노드 : 터미널 기호
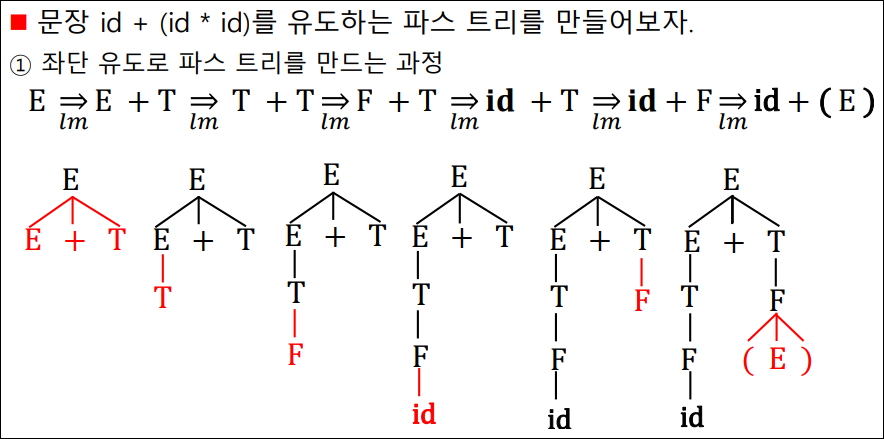
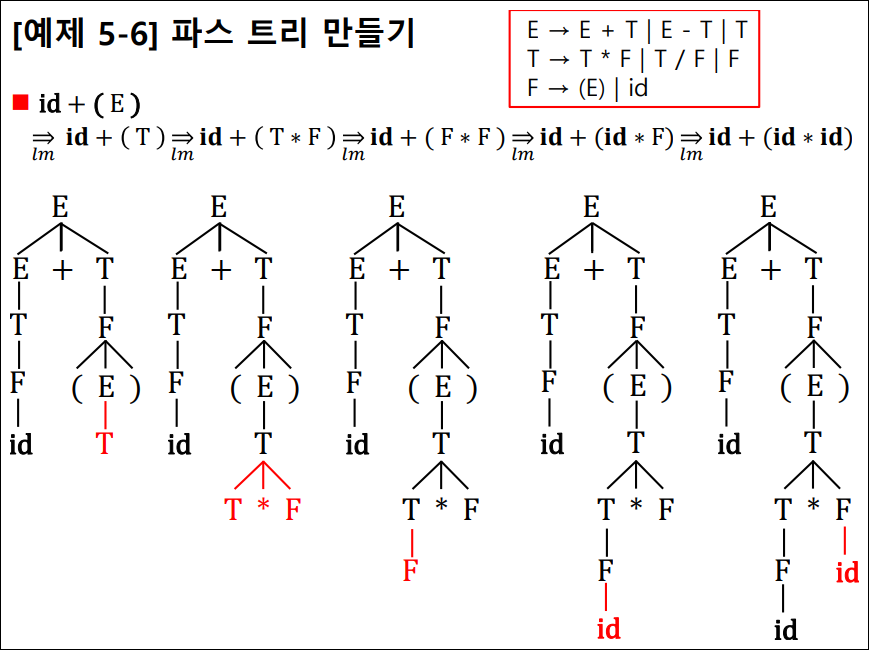
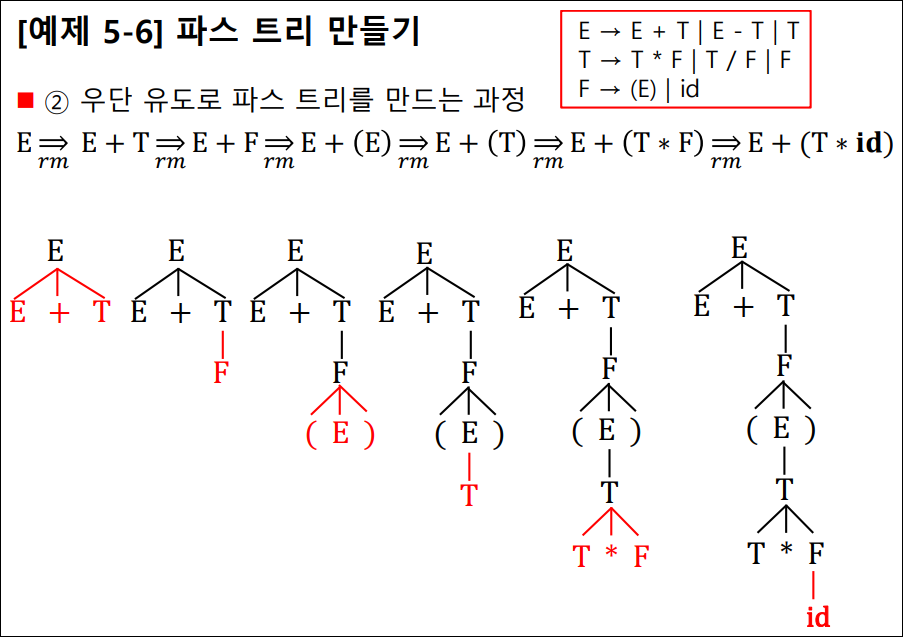
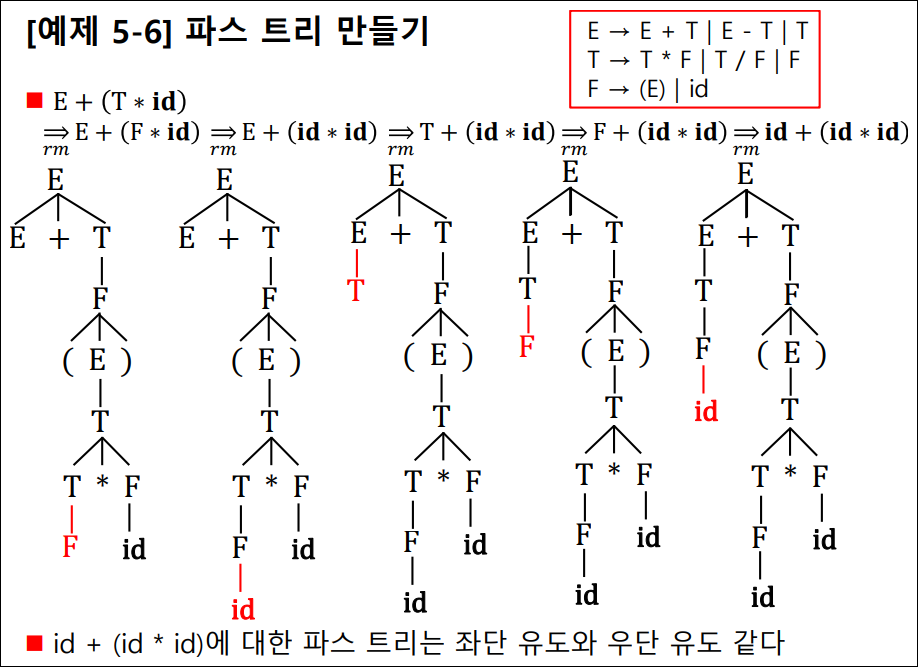
파스 트리 만들기
- E -> E + T | E – T | T
- T -> T * F | T / F | F
- F -> (E) | id
모호한 문법
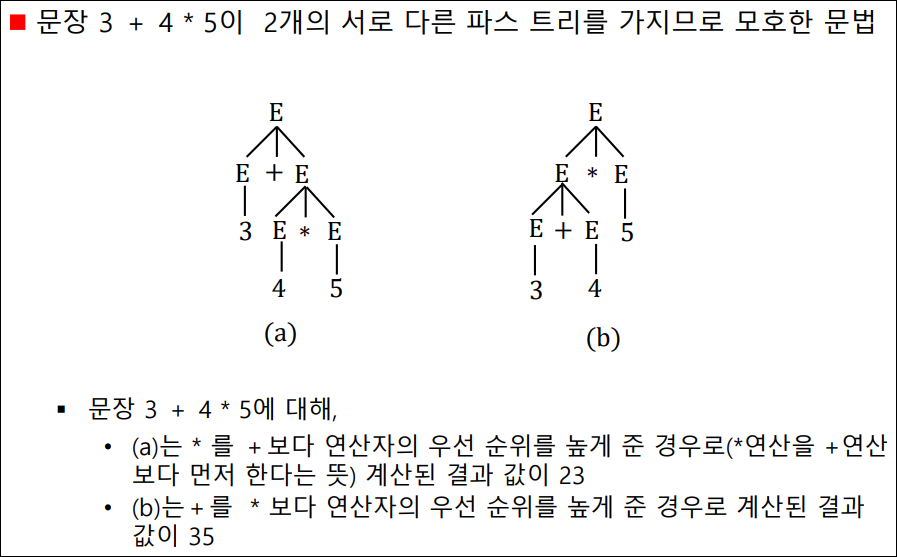
- 모호한 문법
하나의 문장이 서로 다른 두개이상의 파리트리를 갖을때 문법 G는 모호하다라고 표현함
모호한 문법의 예
모호한 문법일 때 파스 트리를 하나로 만드는 방법
- 모호한 문법을 모소하지 않게 변환한 문법으로 구문 분석기를 만들어 처리
- 모호한 문법으로 구문 분석기를 만든 다음 충돌이 생긴 부분을 없앰
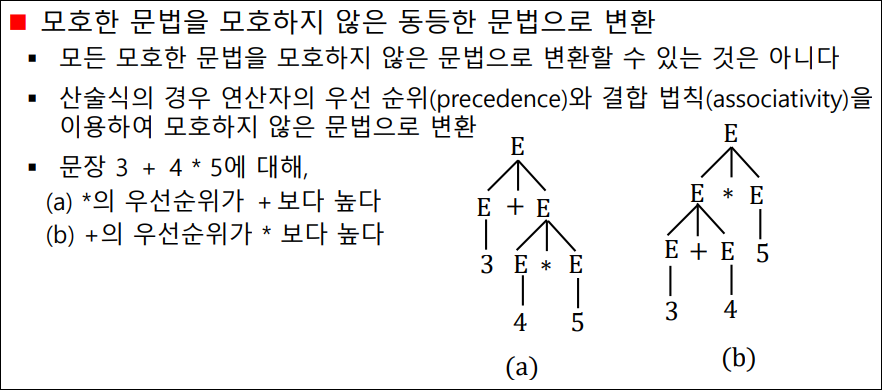
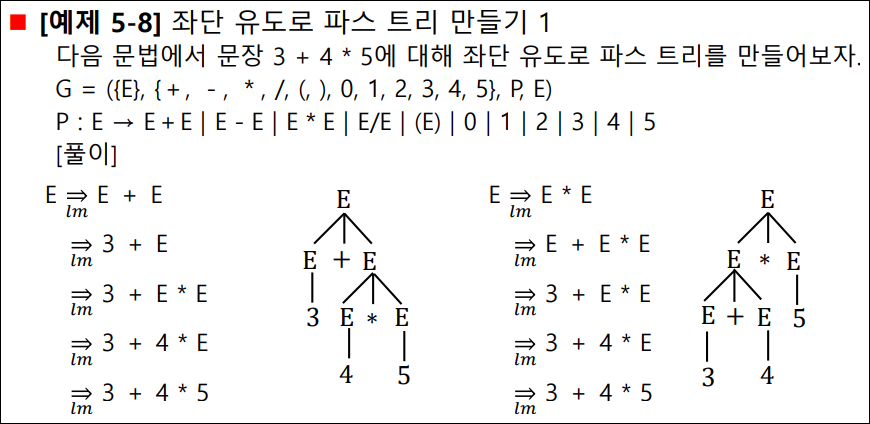
좌단 유도로 파스 트리 만들기 2
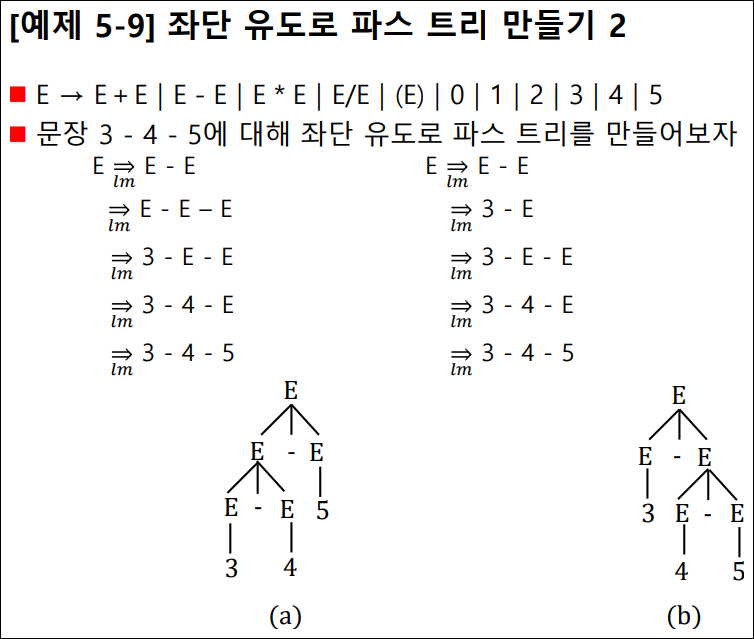
연산자의 우선순위, 결합법칙
- 예: 3 + 4 * 5 를 (3 + 4) * 5와 3 + (4 * 5)로 계산 가능
- 연산의 우선순위는 모호하게 해석가능한 수식에서 어느 연산을 먼저 계산할 것인가를 결정하는 규칙
- 예: 3-4-5 를 (3-4)-5 와 3-(4-5)로 계산 가능
- 연산자의 결합 법칙은 연산자의 우선순위가 같을 때,
- 좌측 결합(left associative): 가장 왼쪽에 있는 연산자부터 계산
- 우측 결합(right associative): 가장 오른쪽에 있는 계산
- 대부분의 프로그래밍 언어에서는 좌측 결합 방식을 취한다.
모호하지 않은 문법으로 변환 예
- E -> E+E | E-E | E*E | E/E | (E) | 0 | 1 | 2 | 3 | 4 | 5
- 모호한 문법에 대해 연산자 우선순위를 *, /, >, +, – 순서로 적용함
- 모든 연산자들이 좌측 결합 법칙을 취하면 모호하지 않은 문법으로 변환 가능
- 아래 그림은 3 + 4 * 5와 3-4-5에 대해 만들어진 유일한 파스트리를 보여줌
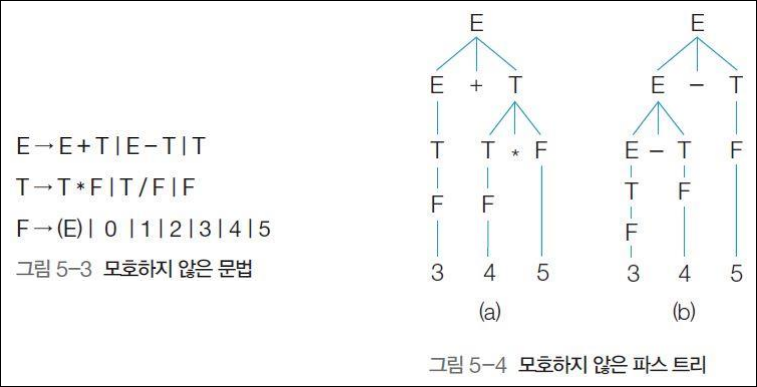

예제: 모호한 문법을 모호하지 않은 문법으로 변환

예제: 현수 else(dangling else)
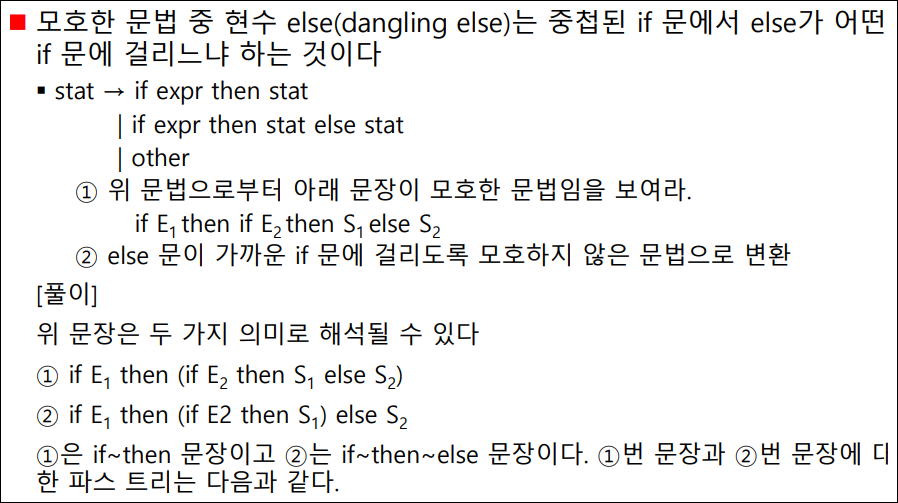
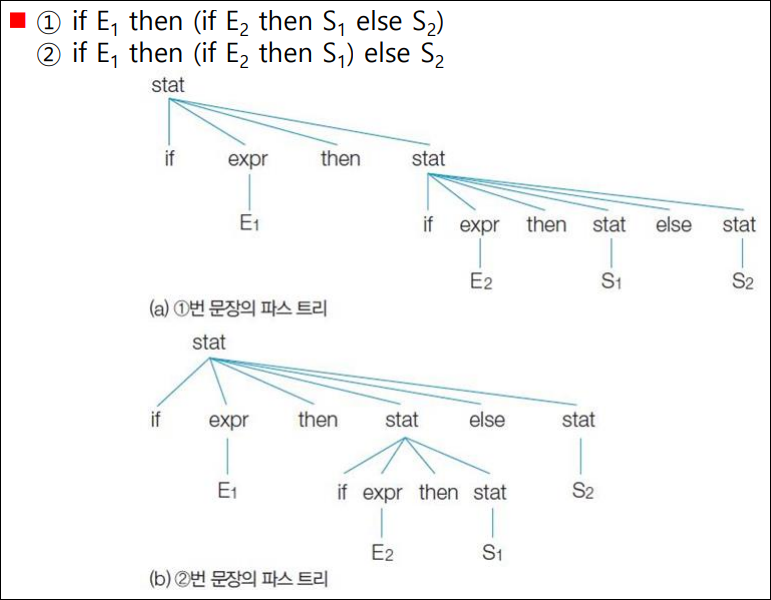
- 하나의 문장에 대해 서로 다른 2개의 파스 트리가 생성되므로 이 문법은 모호한 문법 이다.
- 현수 else를 모호하지 않은 문법으로 변환하는 방법 중 [그림 (a)]와 같이 else를 그 앞에 있는 가장 가까운 if와 연결하는 것으로 일반적인 프로그래밍 언어 에서 사용하는 방법이다.
- 다음과 같은 모호하지 않은 문법으로 변환할 수 있다.

문법 변환
- 문법 변환
- 주어진 문법을 동등한 언어를 생성하는 다른 문법으로 변환
- 비효율 적인 구문분석을 하는 문법을 효율적인 구문분석 문법으로 변환
- 변환 방법
- 불필요한 생성규칙의 제거
- ε -생성규칙의 제거
- 단일 생성규칙의 제거
- 좌인수분해(left-factoring)
- 좌재귀(left-recursion)의 제거 등
불필요한 생성 규칙 (useless production)의 제거

터미널 문자열을 생성할 수 있는 논터미널 기호

예제: 터미널 문자열을 생성하지 못하는 논터미널을 가진 생성 규칙 제거

불필요한 생성규칙 제거

푸시다운 오토마타
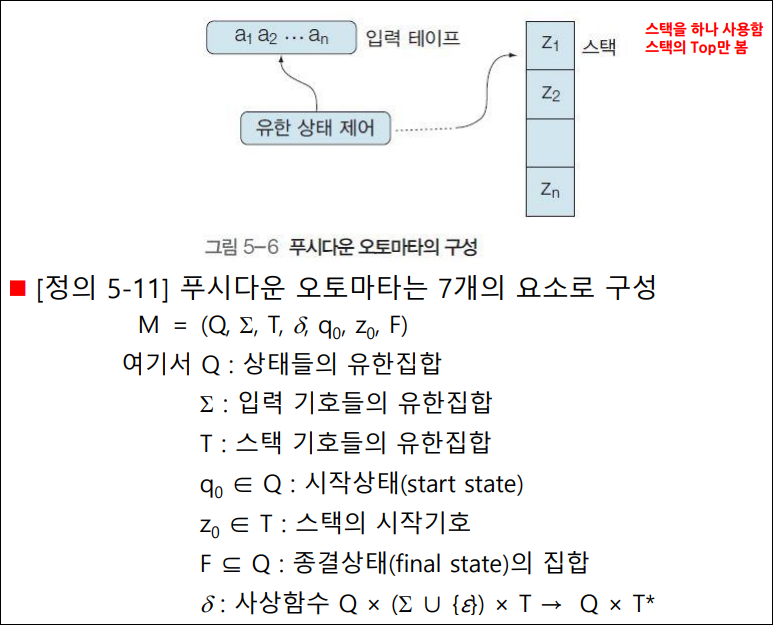
- 정의 : 푸시다운 오토마타는 7개의 요소로 구성
- $M = (Q, \sum, T, \delta, q_0, z_0, F)$
- 여기서 Q : 상태들의 유한집합
- $\sum$ : 입력기호들의 유한집합
- T : 스택 기호들의 유한집합
- $ q_0 \in $ Q : 시작상태
- $ z_0 \in $ T : 스택의 시작기호
- F $\subseteq $ Q : 종결상태의 집합
- $\delta$ : 사상함수 Q × ($\sum \cup $ {$\epsilon$}) × T $\rightarrow$ Q × $T^*$
- (q, a, z) = {(p, r)}이라 하면
- q의 상태에서 입력기호 a를 받았을 때 스택의 톱(top)에 z가 있다면 상태는 p로 이전
- 스택의 톱인 z가 스택에서 삭제(pop)되고 스택에는 r이 삽입(push)되는 것
- 만약 r이 ε인 경우는 스택에서 삭제만이 이루어진다.
- 일반적인 사상함수 δ(q, a, z) = {($p_1$, $r_1$), ($p_2$, $r_2$), ···, ($p_m$, $r_m$)}이라 하면
- 상태는 pi로 전이가 되고 스택의 톱인 z가 삭제되고 스택에는 ri가 삽입
- 이때 입력 제어는 한자리 오른쪽으로 이동
- m=1이면 결정적 푸시다운 오토마타(deterministic push-down automata)
- m ≥ 2이면 비결정적 푸시다운 오토마타(non-deterministic push-down automata)
- δ(q, $\epsilon$, z) = {($p_1$, $r_1$), ($p_2$, $r_2$), ···, ($p_m$, $r_m$)} 이라 하면
- q의 상태에서 입력기호에 관계없이 스택의 톱(top)에 z가 있다면 상태는 p로이전
- 스택의 톱인 z가 스택에서 삭제(pop)되고 스택에는 ri이 삽입(push)되는 것
- 만약 r이 ε인 경우는 스택에서 삭제만이 이루어진다.
- 입력 제어는 이동이 없다
푸시다운 오토마타 #2

예제: 푸시다운 오토마타에 의한 인식 1

푸시다운 오토마타: 푸시다운 오토마타의 확장

요약
- 문맥자유문법
문맥자유문법은생성 규칙이 A $\rightarrow$ $\beta$ 단 $ A \in V_N, \beta \in V^* $ 의형태 - 파스트리
- 좌단 유도: 유도 과정의 각 단계에서 문장 형태의 가장 왼쪽에 있는논터미널 기호를 계속해서 대체^[는 경우
- 우단 유도 : 유도 과정의 각 단계에서 문장 형태의 가장 오른쪽에 있는 논터미널 기호를 계속해서 대체하는 경우
- 좌파스: 하나의 문장을만들 때좌단유도에 의해 적용된 일련의 생성 규칙 순서
- 우파스: 하나의 문장을 만들때우단유도에 의해 적용된 생성 규칙 순서의 역순
- 파스트리 : 문맥자유문법 G에대한파스 트리는 다음과 같음
- 모든노드의 이름은문법 기호
- 루트 노드의 이름은시작 기호 S
- 만약 어떤노드가하나 이상의 자식을가지고 있다면 이노드의 이름은 논터미널 기호
- 왼쪽부터 순서적으로 $X_1$, $X_2$, …, $X_n$의 n개 자식을 가진 어떤 노드 A가 존재한다면 생성 규칙 A $\rightarrow$ $X_1$, $X_2$, …, $X_n$가 존재
- 만약 어떤노드가자식을하나도 가지고 있지 않다면 이노드를 터미널 노드 또는 잎이라 함
- 모호한문법
문법 G에의해 생성되는 어떤문장이 2개이상의 파스트리를 가진 경우문법 G를 모호하다고 함 - 문법변환
- 불필요한생성 규칙: 불필요한기호를 가지고 있는생성 규칙
- 푸시다운오토마타
푸시다운오토마타는유한 상태 제어, 입력 테이프, 무한정의 용량을 가진스택으로 구성됨
