개요

스탠포드대 강의인 cs276 information retrieval의 강의를 공부한뒤 강의 슬라이드를 정리하는 포스팅이다. 어디까지나 자의적인 이해와 해석이 있는만큼 참고할 분들은 비판적 사고로 접근하기를 권장한다.

이번 강의에서는 Scoring, Term Weighting & Vector Space Model에 대해 소개한다.

Recap of Last Lecture

• 컬렉션과 단어의 통계:Heaps’ and Zipf’s laws
• boolean index를 위한 단어 압축
  • 사전을 긴 문자열로 표현, 블럭, front coding
• Postings compression: Gap encoding, prefix-unique codes
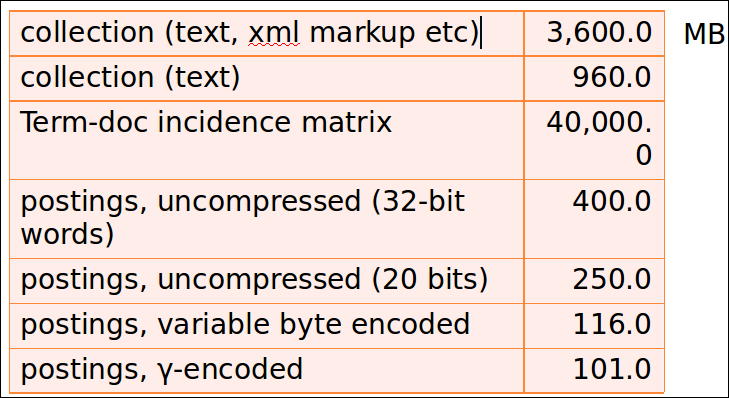
  • Variable-Byte and Gamma codes

OUTLINE

다루게 될 outline이다.

• Ranked Retrieval
• Scoring documents
• Term frequency
• Collection statistics
• Weighting schemes
• Vector space scoring

RANKED RETRIEVAL

• 현재까지는 쿼리가 모두 boolean이다.
  • 문서는 일치하거나 불일치한다.
• 그들의 니즈와 컬렉션에 대해 정확히 아는 전문적인 사용자들에게 좋음
  • 또한 어플리케이션 입장에서도 좋음: 1000개의 결과는 쉽게 소비함
• 하지만 대부분의 사용자에게는 좋지 않음
  • 대부분의 사용자는 boolean 쿼리를 작성하지 못함
  • 대부분의 사용자는 1000개의 결과를 다루기 원하지 않음
  • 특히 웹 검색에서는 이런 경향을 보임

Problem with Boolean search: feast or fam

• boolean 쿼리는 종종 너무 적거나 너무 많은 결과를 리턴함
  • 쿼리 1: “standard user dlink 650” -> 200,000 hits
  • 쿼리 2: “standard user dlink 650 no card found” -> 0 hits
• 적당한 수치의 리턴을 위해 쿼리를 다루는 스킬을 요함
  • AND 조건에 따라 문서가 매우 적게 검색되거나 OR에 의해 너무 많이 검색됨

Quiz 1: Search results

• X AND Y에대해 구글 검색할 때, 총 2000개의 결과가 리턴
• X AND Y AND Z에대해 구글 검색할 때, 총 3500개의 결과가 리턴
• 왜 2번째 쿼리가 더 많은 결과를 리턴하는가?(하나 이상의 가능한 설명을 하시오)

Ranked retrieval models

• 쿼리 표현식을 만족하는 문서의 집합 보다는 ranked retrieval에서는 시스템이 쿼리에 대한 컬렉션에 대한 상위 랭킹의 문서를 리턴함
• free text query: 쿼리 언어의 precise query(연산자나 표현) 보다는 사용자의 쿼리는 한단어 이상의 자연어가 입력된다.
• 요약하자면 2가지 분리된 선택지가 있긴한데 실전에서는 보통 ranked retreival이 free text 쿼리랑 조합된다.

Feast or famine: not a problem in ranked retrieval

랭킹을 메기는 문서의 양을 줄이는 것은 품질면에서는 상용환경에서 큰 이슈가 아니다. 왜냐하면 아래와 같이 구글 검색의 클릭률을 보면 대부분 1페이지의 10개의 검색결과의 클릭률이 94%이다. 유저는 2페이지로 이동할 가능성 조차 낮다.

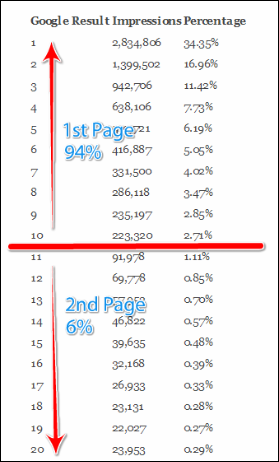
• 시스템이 랭킹이 매겨진 결과를 만들때, 대량의 결과셋 리턴은 이슈가 아님
  • 실제로 결과의 크기는 이슈가 아님
  • 시스템에서는 top k의 결과만 보여줌
  • 우리는 상위 k개의 결과를 보여주어 사용자가 압박을 느끼지 않게함
  • 전제는 랭킹 알고리즘 품질을 좋게 유지하는 것

Scoring as the basis of ranked retrieval

• 우리는 문서가 검색자에게 더 유용할 수 있도록 리턴해주길 원함
• 어떻게 하면 쿼리마다 컬렉션 내의 문서의 랭킹을 정할 수 있을까?
  • 점수값을 [0,1]로 각 문서에 할당한다.
  • 이 점수는 문서가 쿼리에 얼마나 “match”되는가에 대한 척도이다.

Query-document matching scores

• 우리는 쿼리-문서 쌍에 대해 점수를 할당하는 방법이 필요함
• term 한개의 쿼리 부터 시작해보자.
• 만약 쿼리 텀이 문서에서 발생하지 않으면: 점수 0점
• 쿼리 텀이 더 자주 문서에 출현할수록 더 높은 점수를 할당
• 앞으로 이 방식에 대한 몇가지 대안을 살펴볼 예정

Take 1: Jaccard coefficient

• 일반적으로 쓰여지는 A와 B집합의 관계는 아래와 같이 나타냄
  • $jaccard(A,B) = \frac {|A \cap B|} {|A \cup B|}$
  • $jaccard(A,A) = 1$
  • $jaccard(A,B) = 0 \ if A \cap B = 0$
• A와 B가 같은 크기일 필요는 없음
• 항상 0~1 값을 가짐

Quiz 2: Jaccard coefficient

쿼리-문서 match 점수에서 Jaccard coefficient는 어떻게 계산할까?

• Query: ides of march
• Document 1: caesar died in march
• Document 2: the long march

doc1 : $ \frac {1} {6}$ doc2 : $ \frac {1} {5}$ 즉 doc2가 점수가 조금 더 높다.

Issues with Jaccard for scoring

• term frequency를 고려하지 않음 (문서 안에서 얼마나 많이 term이 발생했는지)
• 컬렉션의 희귀한 term은 흔한 term보다 더 유용한데 Jaccard는 이것이 고려되지 않음
• 길이를 normalize 할 더 세련된 방법이 필요함
• 나중에 이 수식을 사용함 $ \frac {|A \cap B|} {\sqrt{|A \cup B|}}$

Recall: Binary term-document incidence matrix

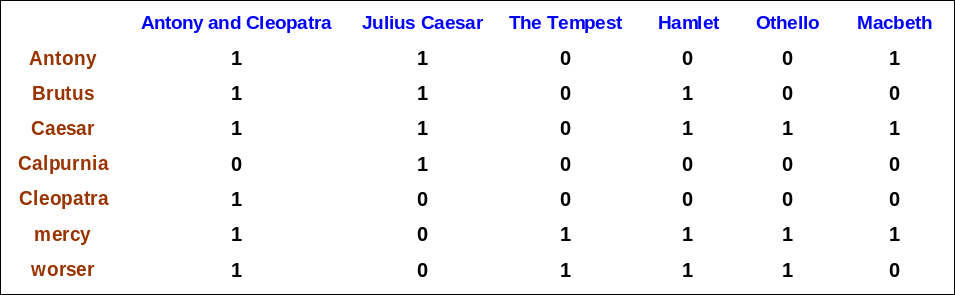
예를 들어 antony and brutus and not(calpurnia)라면

• 110001
• 110100
• 101111 -> 100000

위 비트와이즈 연산을 통해 “Antony and Cleopatra”가 만족하는 소설책임을 찾을 수 있다.

• 각 문서를 바이너리 벡터로 표시함 $ \in ${$0,1$}$^{|V|}$

Term-document count matrices

• 이제 0/1 벡터 대신에 횟수를 벡터화함
• 문서에 term이 등장한 횟수를 고려함
  • 각 문서는 count vector로 표시 in $N^V$

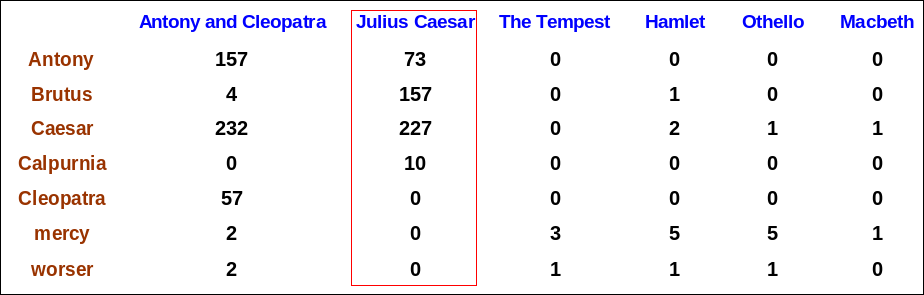
Bag of words model

• 벡터 표현은 문서안의 단어의 순서를 고려하지 않음
• 아래 두 문장은 같은 벡터이다.
  • John is quicker than Mary
  • Mary is quicker than John
• 이것을 BOW 모델이라고 부름
• 사실 이것은 퇴보하는 것인데 왜냐하면 positional index는 두 문서의 차이를 구별할 수 있기 때문이다.
• 나중에 다시 positional 정보에 대해 해결하는 것을 더 얘기하기로 하고 우선은 BOW 모델에 대해 얘기해보자.

Term frequency tf

• $tf_{t,d}$는 문서 d에서 term t가 얼마나 발생했는지를 정의함
• 우리는 tf를 query-document 일치 점수 계산시 쓰고싶은데 어떻게 하면 될까?
• raw tf 값은 우리가 원하는 형탱가 아님
  • tf 10인 문서가 tf 1인 문서보다 더 연관도가 높음
  • 하지만 10배 더 연관있다는 의미는 아님
• 연관도는 tf에 따라 비례적으로 올라가지 않음

Log-frequency weighting

• d 문서의 term t에 대한 log frequency $ w_{t,d} = \begin{cases} 1 + log_{10}{tf_{t,d}}, \ if \ tf_{t,d} > 0 \0, \ otherwise \end{cases}$
• 예제
  • 0 -> 0
  • 1 -> 1
  • 2 -> 1.3
  • 10 -> 2
  • 1000 -> 4
  • etc.
• score = $\sum_{t\in q\cap d}(1+log \ {tf_{t,d}})$
• 문서에서 query term이 하나도 발견되지 않으면 점수는 0이다.

Document frequency

• 희귀한 term은 흔한 term 대비 더 유용함
  • 금칙어를 상기시켜보자.
• 컬렉션에서 희귀한 term이 포함된 query를 생각해보자. (예: arachnocentric)
• 이 term을 포함한 문서는 쿼리 term에 매우 연관도가 높을 것이다. -> 따라서 우리는 이러한 희귀한 arachnocentric같은 term에 가중치를 부여하고 싶다.

Document frequency, continued

• 흔한 term은 희귀한 term 대비 덜 유용하다.
• 컬렉션 내에서 흔한 term을 생각해보자. (예: high, increase, line)
• 이러한 term을 포함하는 문서가 그러지 않은 문서보다는 연관있을 가능성이 높다.
• 하지만 확실한 연관도의 척도는 아님
• frequent term에 있어 높은 positive 가중치를 high, increase, line 단어에 부여해야함
  • 하지만 희귀한 term보다는 가중치를 낮추어야함
• 이를위해 우리는 document frequency df를 활용해야함

idf weight

• $df_t$는 t를 포함하는 문서의 빈도 이다.
  • $df_t$는 t의 정보성에 대한 반비례 측정시 필요한 메트릭이다.
  • $df_t \le N$이다.
• idf(inverse document frequency)는 아래의 수식으로 나타낸다. $ idf_t = log_{10}(N/df_t)$
  • log를 취하는 이유는 idf값을 완화시키기 위함이다.
  • 로그의 base는 그리 중요치 않다.

idf example, suppose N = 1 million

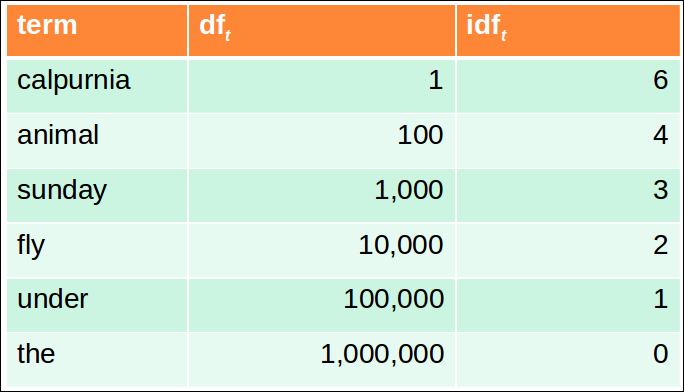
$ idf_t = log_{10}(N/df_t)$

• term 하나당 하나의 idf값이 존재함.
• 쉽게 이해하자면 idf를 적용하면 calpurnia는 prmoting하고 the는 demoting한다.

Effect of idf on ranking

• “iphone”과 같이 idf가 one-term 쿼리에 있어 랭킹에 효과가 있을까?
• idf는 one term 쿼리에 있어서는 효과가 없다.
  • idf는 적어도 2개의 term 이상에 대해 효과가 있다.
  • “capricious person”라는 쿼리가 있으면 idf 가중치는 capricious 라는 희귀한 단어에 person 이라는 흔한 단어 보다 상대적으로 높은 가중치를 부여하게 된다.

Collection vs. Document frequency

• t에 대한 컬렉션 빈도는 전체 컬렉션 내에서 t가 발생한 빈도수를 집계한다. 여러번 등장한 것을 모두 센다.
• 예제

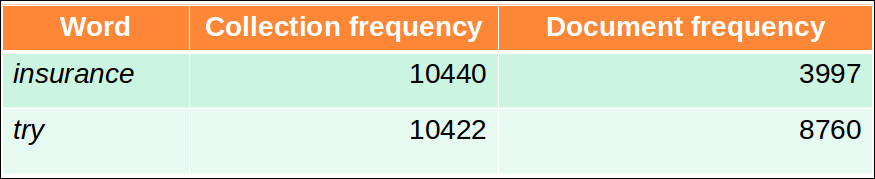
Quiz 3: Collection Frequency

어떤 단어가 더 나은 search term인가?(더 높은 가중치를 받아야 할까?)

idf개념에 의하면 df가 더 낮은 insurance가 더 나은 search term으로 더 높은 가중치를 받아야 할 것이다.

TF-IDF WEIGHTING

• term의 tf-idf 가중치는 tf 가중치 * idf 가중치이다. $W_{t,d} = (1+log_{10}tf_{t,d}) * log_{10}(N/df_t) $

• IR에서 가장 잘 알려진 가중치 공식이다.

  • 노트 : tf-idf에서 “-“는 마이너스가 아니라 하이픈이다.
  • 다른 이름: tf.idf, tf x idf
• 가중치는 문서내의 term 발생빈도에 따라 증가한다.
• 가중치는 컬렉션 내에 term이 희귀할수록 증가한다.

Score for a document given a query

$ Score(q,d) = \sum_{t \in q \cap d} tf.idf_{t,d} $

• 다양한 옵션이 존재
  • 어떻게 “tf”를 계산할것인가(log 적용 여부)
  • 쿼리의 term에 가중치를 부여할지 여부
  • …

Binary → count → weight matrix

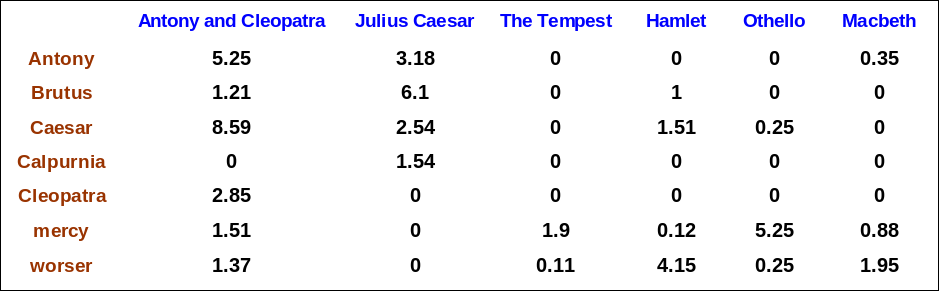
• binary, count를 거쳐 이제 문서는 tf.idf 가중치 메트릭스로 나타낼 수 있다.
• 각 문서는 tf-idf 가중치의 실수값 벡터로 표현된다. $ \in R^{|V|}$

Documents as vectors

• 따라서 우리는 $|V|$ 차원의 벡터 공간을 가짐
• term들은 공간의 차원이다.
• 문서는 공간에서의 점이나 벡터이다.
• 매우 높은 차원: 만약 이 개념을 웹 검색엔진에 적용한다면 수억의 차원이 된다.
• 이건 매우 spares한 벡터이다. – 대부분의 값은 0일 것이다.

Queries as vectors

• 핵심 아이디어
  • 아이디어 1: 쿼리에 대해서도 같은 방식을 적용하여 벡터로 표현한다.
  • 아이디어 2: 공간에서의 쿼리에 대한 문서의 유사도에 대해 랭킹을 매긴다.
• proximity = 벡터의 유사성
• proximity ≈ inverse of distance(거리가 가까울 수록 유사하다는 의미)
• Recall: 이걸 하는 이유가 boolean 모델에서 벗어나기 위해서이다. (앞서 얘기했든 일반인 대상 검색엔진을 만든다면 boolean model은 너무 어렵기 때문)
• 대신에 더 연관있는 문서에 더 높은 랭크를 부여함.

Formalizing vector space proximity

• 2개의 점의 거리를 측정하려면 유클리디안 거리를 사용할까?
• 유클리디안 거리는 다른 길이의 벡터간에는 거리를 잴때 좋은 아이디어가 아니다.
• 왜냐하면 두 벡터가 다른 길이를 가질 수 있기 때문

Why distance is a bad idea

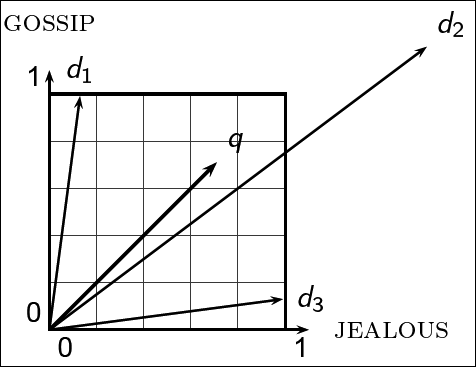
• query q와 문서 d2의 terms의 방향이 매우 유사하더라도 q와 d2의 거리는 매우 멀게 측정된다.

Use angle instead of distance

• 문서 d와 문서 d 내용을 한번 더 문서 끝에 append한 $\hat{d}$가 있다고 가정해보자.
• 의미적으로는 두 문서는 같은 컨텐트를 가지고 있다.
• 유클리디안 거리는 꽤 클것이다.
• 하지만 벡터의 각도는 0이 되고 이는 최대로 유사하다는 뜻이다.

핵심 아이디어: 쿼리와 문서의 term의 벡터 각도에 따라 점수를 매긴다.

From angles to cosines

• 2개의 의미는 동일하다.
  • 쿼리와 문서의 각도가 감소하는 순서로 문서를 정렬함
  • 쿼리와 문서의 코사인 값이 증가하는 순서로 문서를 정렬함
• cosine은 0도에서 180도까지 지속적으로 값이 감소하는 함수이다.

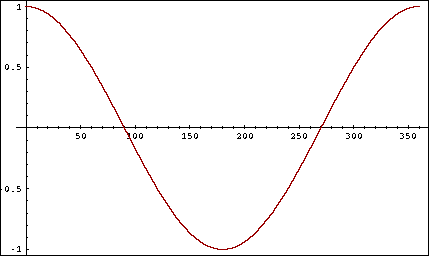
• 하지만 어떻게 또 왜 코사인 값을 계산해야 하는가?

$cos \theta$를 메트릭으로 사용하면 위와 같이 함수 개형이 0도에서 180도로 이동할수록 작아지고 실제 쿼리와 문서와의 관계도 $\theta$가 0이면 1값 180이면 -1이 되니 유사도의 의미가 맞다.

Length normalization

• 벡터는 각각의 컴포넌트를 각 길이로 나뉘어 normalized 될 수 있다. 이를위해 우리는 L2 norm을 사용한다. $ ||\overrightarrow{x}||_2 = \sqrt {\sum_i{x_i^2}}$
• 벡터를 자신의 L2 norm으로 나누는 것은 단위 벡터로 만든다.
• d 와 $\hat d$를 다시 보면 length normalization 이후에는 벡터들이 단위 벡터가 된다. 따라서 두개의 벡터는 같은 벡터가 된다.
  • 이제 길이가 길거나 짧은 문서가 서로 비교가 가능한 가중치를 가진다.

예제를 통해 더 구체적으로 이해해보자. 예를 들어 (3,4,5), (6,8,10)라는 문서 벡터가 있다면 L2 norm을 거치면 아래의 벡터가 된다.

$(\frac{3}{\sqrt{50}}, \frac{4}{\sqrt{50}}, \frac{5}{\sqrt{50}})$ $(\frac{6}{\sqrt{200}}, \frac{8}{\sqrt{200}}, \frac{10}{\sqrt{200}}) = (\frac{6}{4 * \sqrt{50}}, \frac{8}{4 * \sqrt{50}}, \frac{10}{4 * \sqrt{50}}) = (\frac{3}{\sqrt{50}}, \frac{4}{\sqrt{50}}, \frac{5}{\sqrt{50}})$

즉 이를 통해 단위벡터가 됨과 동시에 문서 비교가 가능해졌다.

cosine(query,document)

수식이 복잡해 보이지만 결국 norm을 통해 단위 벡터를 만들고 벡터간 내적을 수행하면 된다.

$$ cos(\overrightarrow q, \overrightarrow d) = \frac {\overrightarrow q \cdot \overrightarrow d}{|\overrightarrow q| |\overrightarrow d|} = \frac {\overrightarrow q}{|\overrightarrow q|} \cdot \frac {\overrightarrow d}{|\overrightarrow d|} = \frac {\sum_{i=1}^{|V|} q_i d_i}{\sqrt{\sum_{i=1}^{|v|}q_i^2} \sqrt{\sum_{i=1}^{|v|}d_i^2}}$$

• $q_i$는 쿼리의 term i에 대한 tf-idf 가중치
• $d_i$는 문서의 term i에 대한 tf-idf 가중치
• $cos(q,d)$는 q와 d의 cosine 유사도 혹은 각도

단위벡터 기준으로는 아래와 같이 간단히 계산된다.

$ cos(\overrightarrow q, \overrightarrow d) = \overrightarrow q \cdot \overrightarrow d = \sum_{i=1}^{|v|}q_id_i$

Cosine for length-normalized vectors

• length-normalized 된 벡터에 있어 cosine 유사도는 단순히 벡터간의 내적이다.

Cosine similarity illustrated

코사인 유사도에 대한 설명 그림이다.

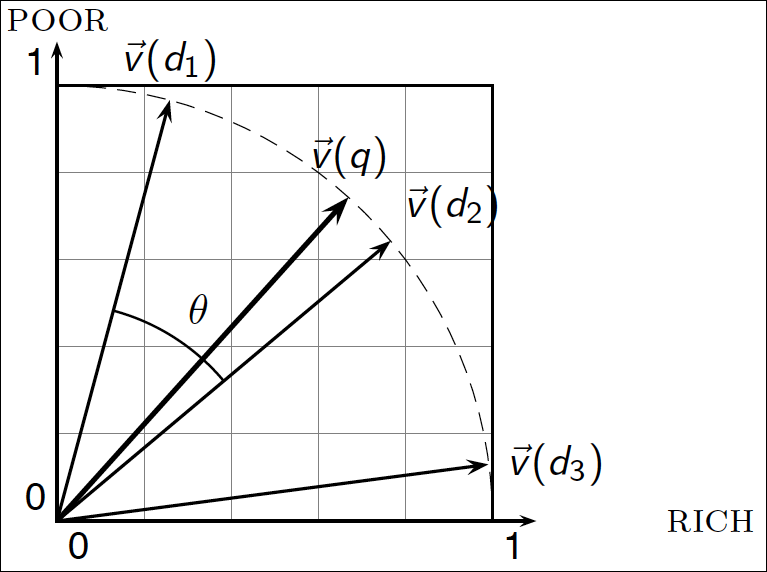
Cosine similarity amongst 3 documents

• 아래의 소설이 얼마나 유사한가?
• SaS: Sense and Sensibility
• PaP: Pride and Prejudice
• WH: Wuthering Heights

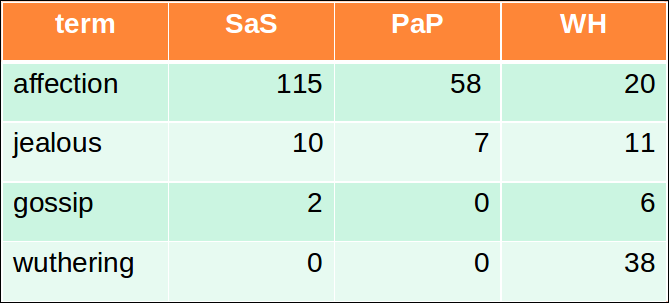
• 노트: 이 예제를 단순화하기 위해 우리는 idf를 고려하지 않는다.

3 documents example contd.

아래는 log frequency로 가중치를 변경 후 norm을 적용하였다.

그러면 예를 들어 SaS의 단위 벡터는 (0.789, 0.515, 0.335, 0)이 된다. PaP는 (0.832, 0.555, 0, 0)이 된다. 따라서 cosine유사도를 문서들 간 계산해보면 SaS와 PaP의 유사도는 0.94가 나온다.

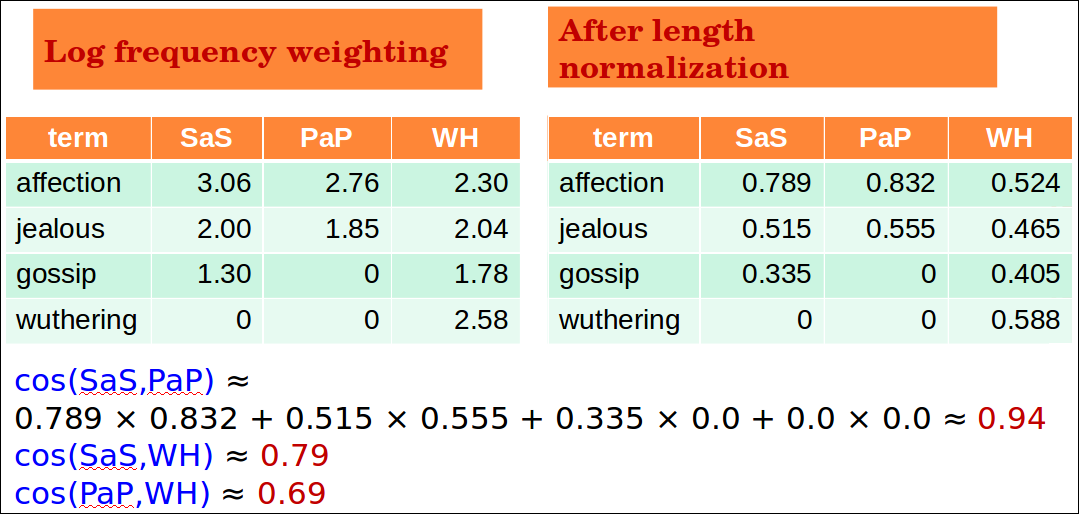
Quiz 4: Novels

• 우리는 왜 cos(SaS,PaP) > cos(SaS,WH) 라고 얘기하는가?
• 하나의 단순한 이유를 적으시오.

cos(SaS, PaP)가 상대적으로 값이 크기 때문이다. cosine값의 범위는 1~-1이고 cos(SaS, PaP)가 1에 더 가깝고 이 말은 각도가 0도에 가깝다는 의미이므로 두 문서가 더 유사하다고 볼 수 있다.

Computing cosine scores

cosine 점수를 구하는 알고리즘이다.

tf-idf weighting has many variants

tf-idf의 가중치 알고리즘 선택의 폭을 아래와 같이 정리한다. 가장 많이 쓰이는 것은 붉은 색 표시가 되어있다.

Weighting may differ in queries vs documents

• 많은 검색 엔진들이 쿼리나 문서에 대해 다른 가중치 부여방식을 허용한다.
• SMART Notation: denotes the combination in use in an engine, with the notation ddd.qqq, using the acronyms from the previous table (앞의 3글자는 문서에 대한 알고리즘이고 뒤의 3글자는 쿼리에 대한 알고리즘이다.)
• 매우 표준적인 가중치 부여 방식으로 lnc.ltc가 있다.
• 문서: lnc의 뜻은 logarithmic tf (l as first character), no idf and cosine normalization 이다.
• 쿼리: ltc의 뜻은 logarithmic tf (l in leftmost column), idf (t in second column), cosine 이다.

quiz: document에 no idf를 적용하는것이 나쁜 아이디어인가?

tf-idf example: lnc.ltc

• 문서: car insurance auto insurance
• 쿼리: best car insurance

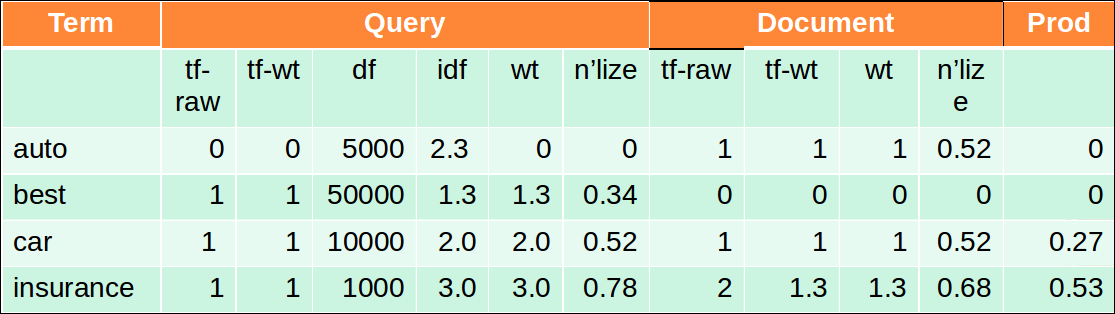
• tf-raw 는 term의 occurence
• tf-wt 는 $ 1+ log(tf_{t,d})$
• df는 $log_{10} \frac {N}{df_t}$
• wt는 tf * idf
• n’lize값은 문서 벡터 길이로 wt를 나눈 것이다. 쿼리와 문서에 대한 각 계산결과인 벡터값이다.

문서 벡터의 길이는 $\sqrt {1^2+0^2+1^2+1.3^2} \simeq 1.92$ 이다. 실제 코사인 유사도는 내적값의 합으로 auto에 대한 내적값 0, best에 대한 내적값 0, car에 대한 내적값 0.27(0.52 * 0.52)과 insurance에 대한 내적값 0.53(0.78 * 0.68)을 더한 0.8이다.

quiz: N이 무엇인가? 문서의 수인가? 맞는것 같다.

Summary – vector space ranking

• 쿼리를 weighted tf-idf vector로 나타냄
• 각 문서를 weighted tf-idf vector로 나타냄
• 쿼리와 문서의 cosine 유사도를 점수로 계산함
• 쿼리에 따라 점수별로 랭킹을 매김
• 사용자에게 top K 문서를 반환함

Scoring and Complete Search System

scoring을 포함한 완전한 검색 시스템에 대해 알아보자.

This lecture

• 벡터 공간 랭킹의 속도 개선
• 완전한 검색 시스템으로 엮음
• 몇가지 잔잔한 주제와 휴리스틱에 대해 배울 필요가 있음

Computing cosine scores

Efficient cosine ranking

• 쿼리와 가장 가까운 top k 문서를 컬렉션에서 찾는 것 = 가장 큰 k query-doc cosine 값
• 효과적인 랭킹:
  • 단일 cosine을 효율적으로 계산
  • k개의 큰 cosine값을 효과적으로 고름 (각도가 작은게 유사도가 높은것을 의미하고 각도가 작을수록 값은 크다.)
  • 이 값을 모든 N cosine을 구하지 않고 구할 수 있을까?

Efficient cosine ranking

• 쿼리 벡터에 대한 knn을 찾는 문제로 바꿔 생각할 수 있다.
• 일반적으로, 우리는 높은 차원에서 이것을 어떻게 효율적으로 수행할 지 알수가 없다.
• 하지만 짦은 쿼리에 대해서는 문제를 풀어볼만 하고 standard index가 이것을 도와준다.

Special case – unweighted queries

• query term에 대해 가중치 부여 안함
  • 각 query term이 한번만 발생하는것을 가정함
• 랭킹에 있어 쿼리 벡터를 normalize할 필요가 없음
  • 이전 슬라이드로부터 조금 단순화함

Computing the K largest cosines: selection vs. sorting

• 일반적으로 우리는 top k 문서를 얻고자 한다.
  • 컬렉션의 모든 문서를 얻고자 하는것이 아니다.
• k개의 높은 cosine값을 골라낼수 있을까?
• J = cosine값이 0이 아닌 문서라고 가정
  • J에서 k개의 최적을 찾는 것이다.

Use heap for selecting top K

• 이진 heap에서 각 노드의 값은 항상 자식 노드의 값보다 큰 형태를 가진다.
• $2J$ 연산으로 생성한 후 k개의 “승자”는 $2log J$ 스텝을 가진다.
• J = 1M, k = 100이면 이건 10% 정도의 정렬 비용을 가진다.

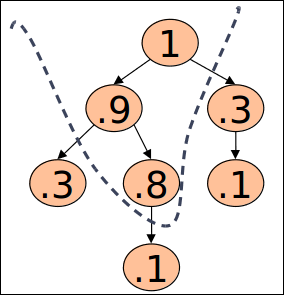
Quiz 5: Heap

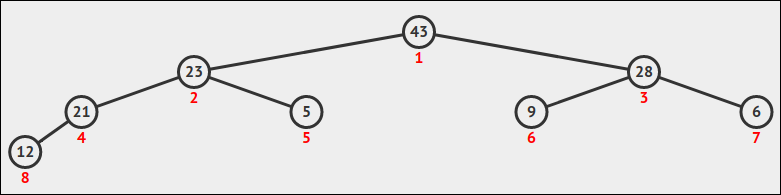
• 이진 max heap을 아래의 키로 만든다: [43, 21, 9, 23, 5, 28, 6, 12]

이 이진 heap을 그려보시오.

Bottlenecks

• 이전 접근법은 완전 일치를 전제로 한다.
• 점수계산에서의 주된 계산 병목은 코사인 계산이다.
• 우리는 이 계산을 피할 수 있을까?
• 그렇다, 하지만 때로는 잘못 될 수 있다.
  • top k에 포함되지 않는 문서가 리턴되는 K개 문서에 포함 될 수 있다.
  • 이것이 나쁜가? 아니다. 이유는 다음 슬라이드.

Cosine similarity is only a proxy

• 사용자는 task와 query formulation을 가진다.
• 코사인은 문서와 쿼리를 매치시킨다.
• 그러므로 cosine은 사용자 만족의 proxy이다.
• 만약 k개의 문서를 top k를 cosine 유사도를 구한것과 비슷하게 구한다면
  • Approximate solution은 용납할만하다.

Generic approach

• K < |A| << N를 만족하는 A 후보군을 찾는다.
  • A는 top k를 반드시 포함할 필요는 없으나 top k문서를 최대한 많이 보유하고 있어야 한다.
  • A에서 top k를 리턴한다.
• A를 가지를 자른 non-contenders로 생각하자.
• 같은 접근법을 다른 scoring 함수에서도 적용 할 수있다.
• 차후 이 접근법을 사용한 다른 scheme을 몇 개 볼 예정이다.

Index elimination

• 기본 알고리즘:
  • cosine 계산 알고리즘은 적어도 하나의 query term을 포함하는 문서만 고려한다.
• 더 확장하면:
  • high-idf query term만 고려한다.
  • 많은 query term을 포함하는 문서만 고려한다.

High-idf query terms only

• “catcher in the rye”라는 쿼리에서
• catcher, rye만 점수를 확보함 (in과 the는 매우 흔한 term이기 때문)
• Intuition: in과 the는 점수에 거의 반영되지 않고 따라서 랭킹을 크게 변경시키지 않음
• 장점: low-idf term들이 많은 문서를 가지고 있을때 이러한 문서를 제거함으로써 시간을 많이 절약할 수 있다.

Docs containing many query terms

• 적어도 하나의 query term과 모든 문서는 top k 리스트 추출 후보이다.
• multi-term 쿼리에서는 적어도 몇개 이상의 query term을 포함하는 문서만 계산한다.
  • 예를 들어 4개중 3개의 쿼리텀을 포함했을 때
  • 웹 검색엔진에서 “soft conjunction”을 권장함
• 포스팅 순회에서 구현하기 쉬움

3 of 4 query terms

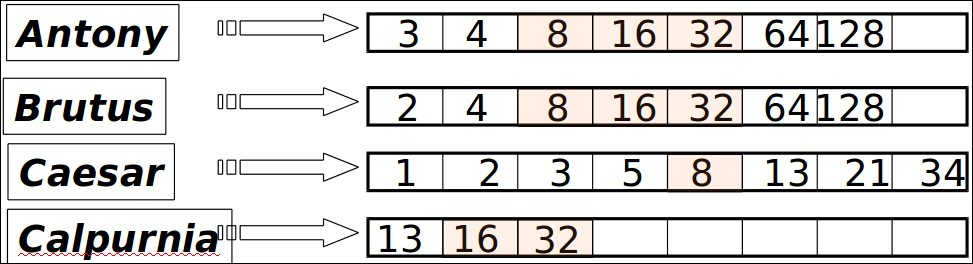
포스팅 리스트를 동시에 순회하면서 교집함은 금새 발견할 수 있음

term이 3개 이상 발생하는 문서 8, 16, 32만 계산함

Quiz 6: Docs containing many terms

위 scheme의 단점이 무엇일까? (예: 많은 쿼리 텀을 포함하는 문서를 필요로 함)

stop word를 제거했더라도 너무 많이 등장하는 phrase 쿼리의 경우 계산 비용이 싸지많은 않을 것 같다.

Champion lists

• 각 term t를 미리 계산해서 t의 포스팅의 가장 높은 가중치인 docs r을 구한다.
  • 이것을 t에 대한 챔피언 리스트라고 부른다.
  • (aka fancy list 또는 top docs)
• r은 인덱스 생성 타이밍에 선택되어야 한다.
  • 그러므로 $ r < K $이다.
  • 왜 r이 k보다 작아도 되는지 이해를 다 못했다.
• 쿼리 타임에는 몇몇 쿼리 term에 대한 챔피언 리스트의 문서만으로 점수를 계산한다.
  • 이중에서 상위 점수의 k 문서를 선택한다.

Static quality scores

• 우리는 상위 랭킹 문서가 relevant 하고 authoritative 했으면 한다.
• Relevance는 코사인 점수에 의해 모델링된다.
• Authority는 일반적으로 문서의 쿼리 독립적인 프로퍼티이다.
• authority 예제
  • 위키피디아(다른 웹사이트와 비교하여)
  • 인용이 많이 된 뉴스 기사
  • 페이지 랭크
• authoritative 하다는 것의 의미는 문서 자체가 쿼리 텀에 독립적으로 질이 좋은 문서인지를 가늠하는 척도이다.

Modeling authority

• 각 문서를 쿼리 독립적인 품질 점수를 [0,1]로 각 문서 d에 부여한다. $ g(d)$로 정의한다.
• 예를들어, 인용되는 수를 [0,1]로 스케일하여 부여하여 사용한다.

연습: $ g(d)$의 수식을 제안해 보시오.

Net score

단순한 합산 점수를 고려하는 것인 코사인 유사도와 authority를 조합하는 것이다.

• $ net$-$score(q,d) = g(d) + cosine(q,d) $
  • 우리는 선형결합을 수행할 수 있을까?
  • 사실, 사용자 만족도에 대한 어떠한 2개의 시그널에 대한 함수를 의미한다.
• 이제 net score를 통해 top k 문서를 찾아보자.

Top K by net score – fast methods

• 첫번째 아이디어: 모든 포스팅을 $g(d)$로 정렬함 나타냄
• 키: 모든 포스팅에 대한 일반적인 순서가 있다.
• 그러므로, 동시에 query term의 포스팅을 순회하며 포스팅 간의 코사인 유사도를 계산할 수 있다.
  • 포스팅 교집합
  • 코사인 점수 계산

Why order postings by g(d)?

• $g(d)$ 정렬에서 상위 점수의 문서는 포스팅 순회에서 일찍 나타난다.
• 시간 제약이 있는 어플리케이션(예를 들어 50ms안에 무조건 서비스 해야함)에서, 위 방법은 포스팅 순회를 일찍 끝낼수 있게 해준다.
  • 모든 문서의 포스팅에 대해 적은 점수계산이 일어난다.

Champion lists in g(d)-ordering

• $g(d)$-ordering을 챔피언 리스트랑 조합할 수 있을까?
• 각 term에 대한 챔피언 리스트인 r docs를 높은 $g(d)$와 $tf$-$idf_{td}$ 기준에서 뽑아놓는다.
• 챔피언 리스트에 있는 문서만으로 top k 결과를 탐색한다.

High and low lists

• 각 term에 대해, 2개의 포스팅 리스트를 유지하는데 high, low라고 부른다.
  • high는 챔피언 리스트라고 생각하자.
• 쿼리에 대한 포스팅을 순회하면서 high list를 우선 탐색한다.
  • 만약 k 이상의 문서가 있으면 k개만 선택하고 멈춘다.
  • 아니라면 (그리고 시간 제약이 덜하다면) low 리스트의 문서를 획득한다.
• 단순하게는 $g(d)$를 빼고 코사인 점수만을 사용할수도 있다.
• 이 의미는 index를 2개의 세그먼트 티어로 나눈다는 의미이다.

Impact-ordered postings

현재까지: global ordering과 동시 순회에 대해 알아보았다.

• $tf_{t,d}$가 충분히 높은 문서에 대해서만 점수계산함
• $tf_{t,d}$의 포스팅 리스트를 정렬하고 싶음
• 현재: 모든 포스팅이 공통의 순서로 정렬되어 있지 않음
• top k를 뽑기 위해 어떻게 점수를 계산해야 할까?
  • 2개의 아이디어가 있음

1. Early termination

• t의 포스팅을 순회할 때 아래의 조건을 만족할 때 멈춤
  • 고정된 수치의 r 문서가 발견될때 멈춤
  • $tf_{t,d}$가 특정 threshold 밑으로 떨어짐
• 각 쿼리 term의 포스팅 결과셋을 합침
  • 각 쿼리 term의 포스팅을 하나로
• 이렇게 합쳐진 문서의 점수만 계산함

2. idf-ordered terms

• query term의 포스팅을 고려할 때 내림차순 idf로 고려함
  • 높은 idf term은 점수에 상당히 반영될 여지가 높음
• 각 query term에 대해 점수를 업데이트 함에따라 점수가 상대적으로 변하지 않으면 멈춤
  • 즉, idf순으로 term을 정렬해놓고 점점 점수가 바뀌지 않으면 뒤쪽 term은 아예 거들더 보지도 않는 개념이다.
• term에 대한 정렬은 cosine 유사도나 net score를 적용할 수도 있음

Cluster pruning: preprocessing

• $\sqrt{N}$개 문서를 랜덤으로 뽑는데 이를 리더라 부른다.
• 모든 다른 문서에 대해 리더와 가까운 문서들을 미리 계산한다.
  • 이를 followers라 부르고 리더에 문서를 붙인다.
  • 가능성: 각 리더는 $\sqrt{N}$의 followers를 가질 가능성이 있다.

Cluster pruning: query processing

• 쿼리를 아래와 같이 처리함
  • query Q에 대해 가까운 리더 L을 찾아냄
  • k개의 L을 따라는 follower를 찾아냄

Visualization

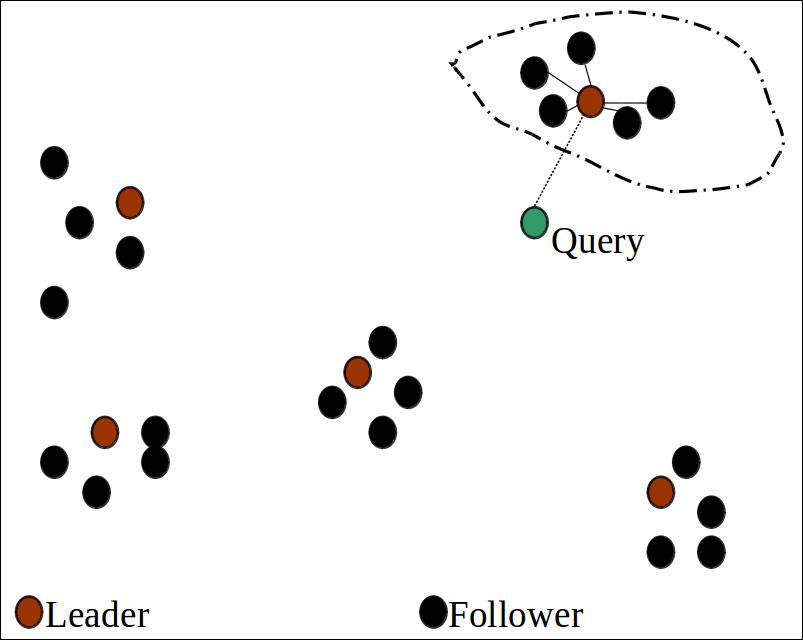
갈색은 리더, 검은색은 follower이다. 초록색 쿼리가 들어왔을 때 가장 가까운 클러스터의 문서를 조회한다.

Why use random sampling

• 빠르다.
• 리더는 data 분포를 반영한다.

General variants

• 이 기법은 아래와 같이 변형되어 응용될 수 있다.
• 각 follower는 b1=3(black 색깔의 1명의 follower가 리더를 1명이 아닌 3명을 따름)의 리더 가까이 붙여진다.
• 쿼리로부터 b2=4의 가까운 리더와 follower를 찾아낸다. -> 이렇게 리더를 여러명 찾아내는 방법은 문서를 더 많이 붙여 recall을 좀 더 올릴 가능성이 있다.
• 리더/follower 생성을 반복한다.

Quiz 7: Nearest leader

주어진 쿼리에서 리더를 찾기위해서 얼마나 많은 코사인 계산이 필요한가?

• $N$
• $N logN$
• $N^2$
• $\sqrt N$

Parametric and zone indexes

• 현재까지 문서는 term의 순서였다.
• 사실 문서는 여러 부분이 존재하는데 일부는 특별한 의미를 지닌다:
  • Author
  • Title
  • Date of publication
  • Language
  • Format
  • etc.

이러한 것들이 문서의 메타데이터를 구성한다.

Fields

• 우리는 가끔 메타데이터 검색을 필요로 한다. 예: find docs authored by William Shakespeare in the year 1601, containing alas poor Yorick
  • 1601이라는 연도 필드에서 검색
  • 저자의 lastName 필드로부터 shakespeare를 검색
• 필드 또는 파라미터 index: 각 필드값에 대한 포스팅
  • 때때로 range tree를 만들어야 함(예: dates)
• 필드 쿼리는 일반적으로 교집합으로 다뤄짐
  • 문서는 반드시 shakespeare가 저자여야함

Zone

• zone은 text 내에서 특정 일부의 영역이다.
  • Title
  • Abstract
  • References …
• zone에 대해 역색인을 만들어 zone도 조회가 가능케 한다.
• 예: 제목 영역에서 merchant를 찾고 “gentle rain”을 쿼리한다.

Example zone indexes

• 사전 방식의 zone 인코딩
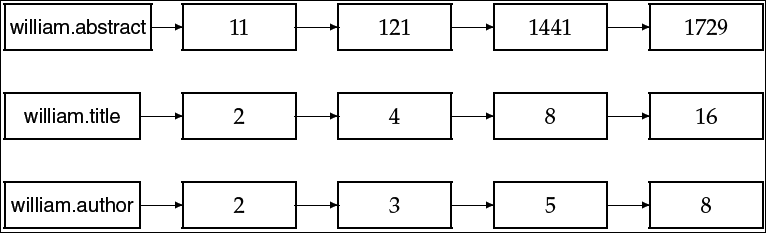
• 포스팅 방식의 zone 인코딩

Tiered indexes

• 포스팅을 쪼개 리스트의 계층으로 나눈다.
  • Most important
  • …
  • Least important
• $g(d)$나 다른 측정법에 의해 완성됨
• 역색인은 그러므로 티어로 쪼개져 티어가 낮아질수록 중요도가 낮아짐
• 쿼리 타임에 top tier를 사용한다.(k개를 찾는데 실패하지 않는다면)
  • 만약 그렇다면 low tier로 내려감

Example tiered index

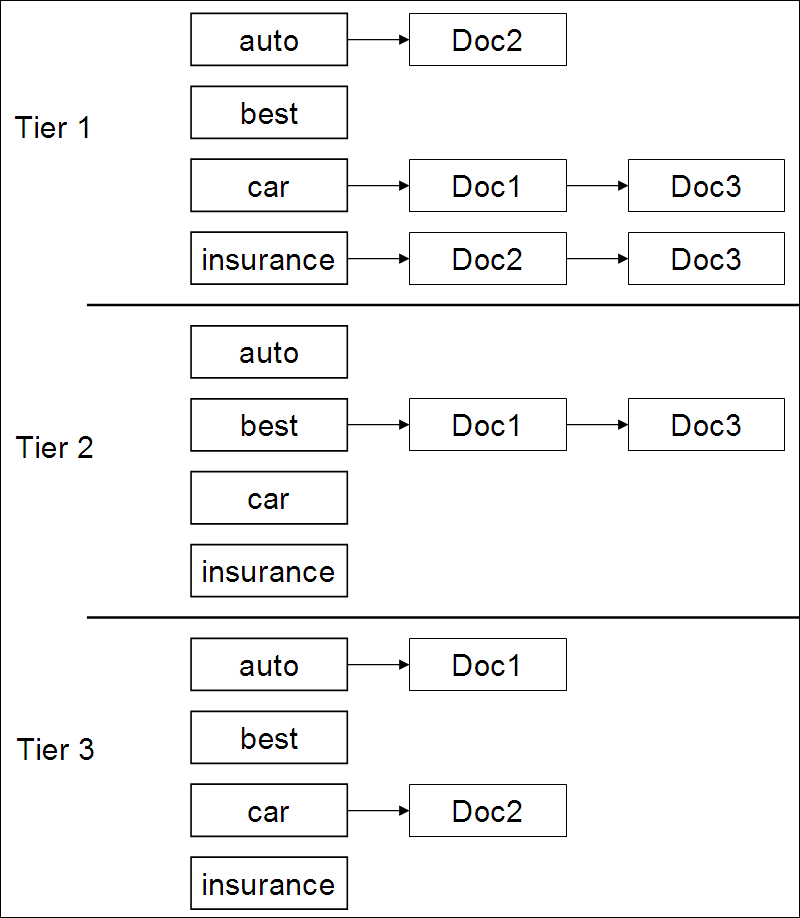
각 티어마다 같은 term의 구성이 있고 각 term마다 포스팅 리스트를 가진다. auto에 대해서는 doc2가 높은 티어1 에 속해있고 car라는 단어에 대해서는 낮은 티어 3에 속해있다.

Query term proximity

• Free text queries: term들의 집합이 검색창으로 들어옴 – 웹에서 흔함
• 사용자는 쿼리 텀들끼리 서로 가까이 있는 문서를 선호함
• w를 문서내에서 모든 쿼리 텀을 포함하는 가장 작은 윈도우로 정의해보자.
  • “strained mercy”를 쿼리하면 문서에 “mercy is not strained”가 있다면 w는 4이다. (단어수 기준)
• 점수 계산 함수를 여기다 어떻게 고려할수 있을까?

Query parsers

• 사용자의 free text 쿼리는 하나 이상의 쿼리를 index에 질의할 수 있음 예: “rising interest rates”를 쿼리
  • 쿼리를 phrase query로 실행함
  • 만약 phrase를 포함하는 문서수가 K보다 작다면 “rising interst rates”를 “rising interst”와 “interest rates”로 나누어 질의한다.
  • 만약 여전히 k보다 작은 문서가 리턴된다면 매칭되는 문서를 벡터화 하여 질의한다.
• 이것의 순서는 쿼리 파서에 의해 발행된다.

Aggregate scores

• 우리가 보기에 점수계산 함수는 cosine, static quality, proximity 등을 다 조합할 수 있다.
• 최적의 조합은?
• 몇 어플리케이션은 전문가의 튜닝이 필요하다.
• 머신러닝 방법이 점점 일반화 되고 있다.
  • 이후 강의에서 다룸

Putting it all together

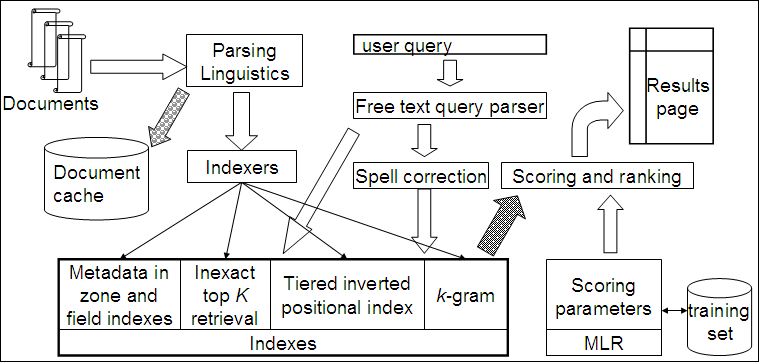
Components we have introduced thus far

• Document preprocessing (linguistic and otherwise)
• Positional indexes
• Tiered indexes
• Spelling correction
• k-gram indexes for wildcard queries and spelling correction
• Query processing
• Document scoring
• Term-at-a-time processing

Components we haven’t covered yet

• 문서 캐시: 스니펫을 생산할 필요가 있음(동적 summary)
• zone indexes: index들을 다른 zone으로 분리함: 문서의 body, 하이라이트된 text, anchor, 메타데이터 등
• 머신러닝 랭킹 함수
• 유사도 랭킹
• 쿼리 파서

Vector space retrieval: Interactions

• phrase retrieval을 vector space retrieval과 어떻게 조합할 수 있을까?
• df/idf를 모든 가능한 phrase를 전부 다 계산하고 싶지 않다. 왜? 너무나 많은 조합의 계산을 수행해야 하기 때문
• boolean retreival을 어떻게 벡터 공간 획득과 조합할 수 있을까?
  • 예: “+”, “-“
• 사후 필터링은 간단하지만 비효율적이다. (쉬운 답이 없다.)
• 어떻게 와일드카드를 벡터 공간 획득과 조합할 할 수 있을까?
• 쉬운 답이 없다.