개요
Centrality measures in spatial networks of urban streets 논문을 요약하여 정리한다.
소개
도시의 거리 패턴을 이용해서 어떤 특징이 있고 분류를 할 수 있는지는 논한다. 도시의 공간적인 거리를 그래프화 하고 특징을 확인한다. 총 4가지의 Centrality를 이용하고 계획적 도시와 자생적으로 생겨난 도시의 차이에 대해 말한다.
Sample of Analysis
- 18개의 다른 도시의 1평방 마일의 공간을 표본으로 한다.
- 도시 네트워크의 공간을 그래프화 한다.
- 비방향성의 가중치를 지닌 그래프로 나타낸다.
용어정의는 아래와 같다.
- 노드 : 교차로
- Edge : 거리
- N : 노드의 수
- K : edge의 수
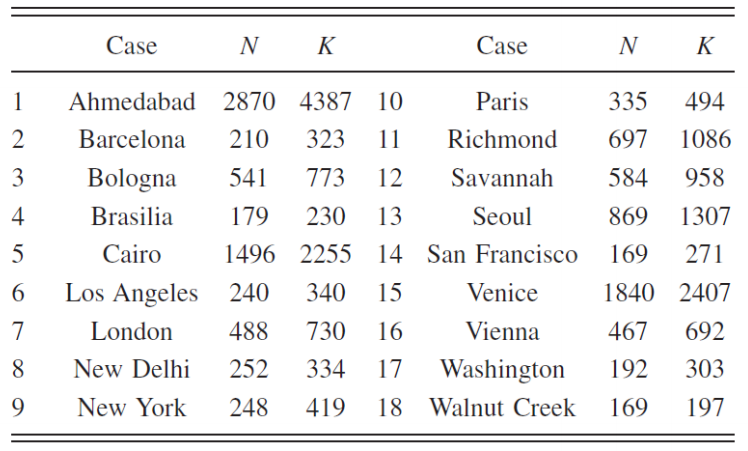
아래 도표는 샘플도시의 종류 및 N과 K값이다.
Centrality 종류
아래의 4가지 종류의 Centrality를 이용하고 있다.
- Closeness centrality
- Betweenness centrality
- Straightness centrality
- Information centrality
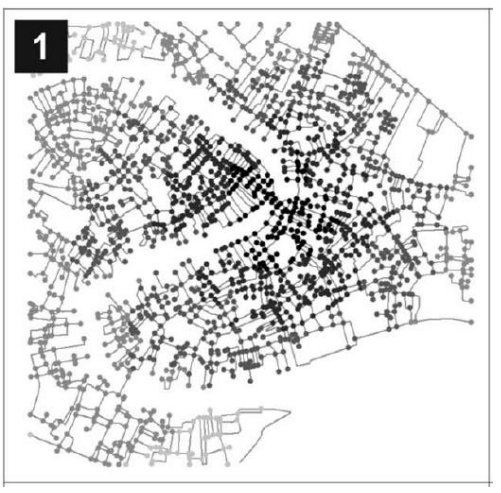
Closeness Centrality
Closeness Centrality에 대해 간단히 알아보면 수식은 아래와 같고 특정 i노드에 대한 CC는 i가 아닌 노드로 가는 최단거리 경로를 다 합하여 이를 $ N – 1 $ 노드수로 나눠주는 것이다.
$ C_i^C = \frac {N-1}{\sum_{j \in G;j \ne i}d_{ij}} $
Betweenness Centrality
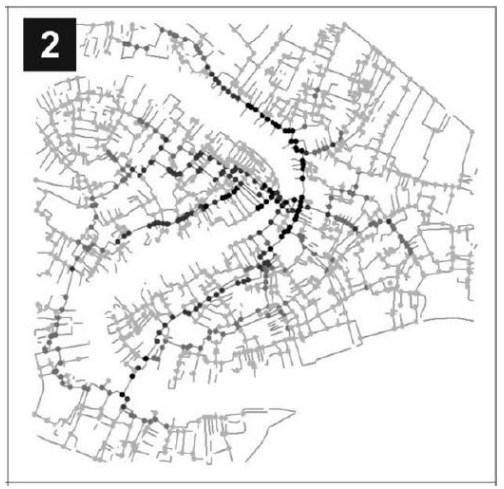
Betweenness Centrality의 수식은 쉽게 설명하자면 j노드에서 k노드 까지 가는 경로의 갯수를 다 더한값을 i노드를 경유하여 j노드에서 k노드를 가는 최단경로의 갯수로 나눈것이다.
$ C_i^B = \frac {1}{(N-1)(N-2)} \sum_{jk \in G, j \ne k \ne i} n_{jk}(i)/n_{jk}$
Straightness Centrality
모든 노드에 대해 수식은 i와 j의 거리를 i와 j의 유클리드의 거리로 나눈값의 합을 $ N -1 $로 나눈 값이다.
수식에서 $ Eucl$은 유클리드 거리를 의미하고 구하는 방법은 i와 j에 가상의 직선을 그어 거리를 대략 구한다.
$ C_i^S = \frac {1}{N-1} \sum_{j \in G, j \ne i} d_{ij}^{Eucl}/d_{ij}$

Information Centrality
$ E $는 Efficiency를 의미한다. 이부분은 제대로 이해를 하지 못했다.
$ C_i^I = \frac {\Delta E}{E} = \frac {E[G] – E[G’]}{E[G]}$
$ E[G] = \frac {1}{N(N-1)} \sum_{i,j \in G, i \ne j} d_{ij}^{Eucl}/d_{ij}$
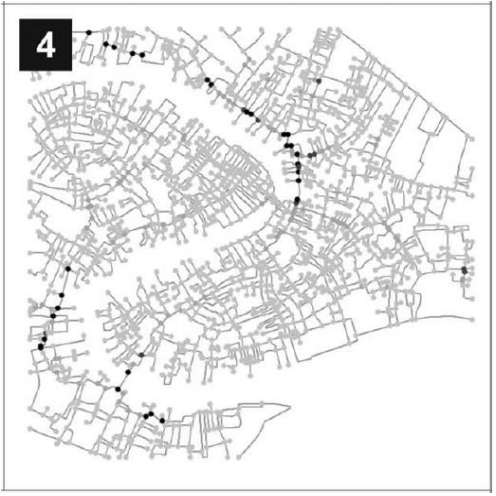
Spatial distiribution of centralities
정리하자면 4가지의 Centrality로 표현한 그림은 아래와 같다.

Evaluation
분석을 해보니 계획된 도시는 지수분포 후자의 경우 가우시안 분포를 나타내고 있었다. 계획도시는 확률분포 p가 0.1 ~ 0.3 사이로 나타나는 것을 알 수 있었다.
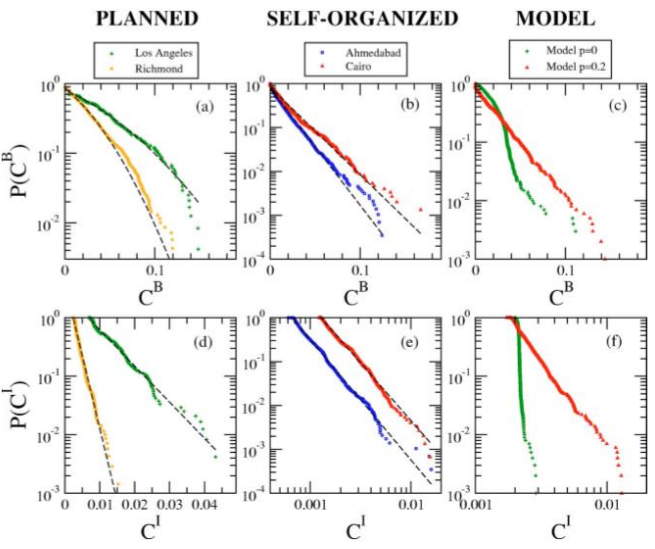
지니계수를 보면 도시들은 아래와 같이 나타낼 수 있다.
- NewYork : 0.12
- Richmond : 0.19
- Cairo : 0.2
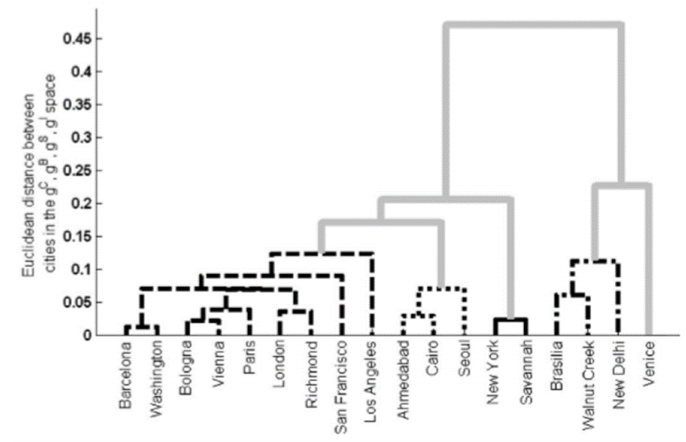
지니계수 계산법으로 Centrality Measure를 계수화 하여 Clustering 해보면 아래의 그림과 같이 군집이 일어난다.
Conclusion
- 각각의 Centrality 측정법은 공간상의 중심에 대한 의미를 다르게 부여하고 있다.
- Centrality 측정법을 통해 다른 도시간의 유사성을 엿볼수 있다.
- 이 지표들은 도시를 새로 계획할때 수치적 정보를 제공해 줄 수 있다.