개요
Anomaly detection in data represented as graphs 논문에서 얘기하는 그래프 기반 비정상 패턴을 찾기위한 접근법을 알아보고 GBAD-MDL, GBAD-P, GBAD-MPS 알고리즘을 설명한다.
논문 원문 링크
비정상 패턴 유형
그래프에서 찾아내는 비정상 패턴의 유형을 아래와 같이 정의한다.
- 예상치 못한 vertex가 존재함
- 예상치 못한 edge가 존재함
- vertex의 label의 예상과 다름
- edge의 label이 예상과 다름
- 있어야할 vertex가 없음
- 있어야할 두 vertex 간의 edge가 없음
그래프에서는 비정상 패턴이 Insertion/Modification/Deletion 에서 일어날 수 있다. Insertion은 1~2, Modification은 3~4, Deletion은 5~6에서 일어날 수 있다.
가정
논문에서는 아래와 같은 가정을 가진다.
- 가정 1 : 대부분의 그래프 패턴은 정상 패턴을 띈다. 오직 X%만이 정상패턴의 변형된 유형을 가질 것이다.
논문의 비정상에 대한 정의 자체가 정상 패턴의 약간의 변형을 비정상 시도라고 보기 때문에 위의 가정을 얘기한다.
- 가정 2 : 그래프는 정규화 되어있다.
그래프가 비정규화 되어 있으면 비정상과 noise 사이의 구별이 어렵기 때문이다.
- 가정 3 : 비정상 패턴은 하나 이상의 그래프의 insert/modification/deletion을 가진다.
그래프에서 변형이 일어날 수 있는 연산은 위의 3가지이다. 따라서 정상패턴의 변형은 위의 3가지 연산으로 구성되어 있다.
- 가정 4 : 정상 패턴은 연결되어 있다.
논문에서 실생활의 활용 예제로 고려한 데이터들인 화물 운송, 통신사 트래픽, 금융 거래 등은 모두 노드와 링크가 모두 연결되어 있다.
- 가정 5 : 그래프의 정상패턴의 편차가 잘 표현되어 비정상 패턴의 편차가 잘 구별 될 수 있다.
논문은 충분한 데이터를 확보하여 (편차가 고려된)실제 정상 패턴을 얻지 못하면 비정상 패턴을 탐지하는데 어려움이 있을수 밖에 없다.
Graph-based anomaly detection algorithms
대부분의 비정상 탐지 방법은 지도 학습법으로 접근한다. 즉, 어떤 비교나 학습이 수행되어야 할지 기준점이 되는 정보가 필요하다. 그러나 이러한 접근법의 한계점은 데이터를 미리 확보하여 학습을 시켜야 한다는 것과 데이터가 이미 라벨링(정상/어뷰징) 되어 있어야 한다는 점이다.
논문에서는 GBAD를 이용하여 3개의 알고리즘을 개발하였다. GBAD는 비지도 학습법으로 SUBDUE 그래프 기반 탐지 시스템 기반으로 구현되었다. 너비 위선 탐색과 MDL 휴리스틱(해석하자면 threshold를 정하는 것)을 이용한 GBAD를 사용한 3개의 알고리즘은 입력된 그래프의 정상 패턴을 발견하고 이를 활용하여 비정상 패턴을 탐지한다.
논문의 구현체에서는 MDL 접근법이 아래의 수식을 최소화 할수 있는 가장 적합한 부분 구조를 찾아낸다. 논문에서 정의한 Notation은 아래와 같다.
$ M(S,G) = DL(G|S) + DL(S) $
$ G $ = 전체 그래프
$ S $ = 부분 구조
$ DL(G|S) $ = S를 이용해 압축된 G의 description length
$ DL(S) $ = 부분 구조의 description length
논문에서 개발한 3가지의 알고리즘은 GBAD-MDL,GBAD-P, GBAD-MPS 이다.
논문에서 얘기하는 SUBDUE 시스템 및 MDL의 개념은 SWF 설명를 참고하면 무척 도움이 된다.
해당 플래시파일을 먼저 이해하고 논문을 읽어야 이해가 된다.
필요하면 SUBDUE 시스템 분석를 참고한다.
Information theoretic algorithm (GBAD-MDL)
GBAD-MDL 알고리즘은 MDL 방법을 사용하여 그래프 안에서 가장 적합한 부분구조를 찾고 차례로 모든 부분 구조에서 비슷한 패턴을 찾는다. 추상화 해서 설명하자면 그래프 G가 있다고 가정할때:
- 가장 적합한 부분구조 S를 찾는데 S는 G의 MDL이다.
- 모든 I인스턴스를 찾는데 I는 특정 임계치 이하의 변형 비용을 가진다. 임계치는 사용자가 정의한다. 변형 비용의 기준은 S가 기준 그래프이다.
- 최종 출력값은 모든 I에 대해 비용 * 빈도가 최소화 되는 값을 가진 I를 출력으로 간주한다.
“변형 비용”은 그래프 A가 그래프 B가 되기위해 필요한 vertex 혹은 edge를 하나 바꿀때마다 1.0씩 증가시킨 값이다. 여기에서의 변형비용은 가장 적합한 부분구조 S로 변형하기 위해 들어가는 비용이다. 최종 결과는 이 변형 비용 및 빈도이다. 변형비용 및 빈도가 독립적인 변수이기 때문에 2개의 값을 곱한다. 최종값이 적은값일수록 구조는 더욱 비정상적이라고 볼 수 있다.
예제
논문에 나와있는 아래와 같은 그림이 있다면 위의 접근법은은 아래와 같아진다.
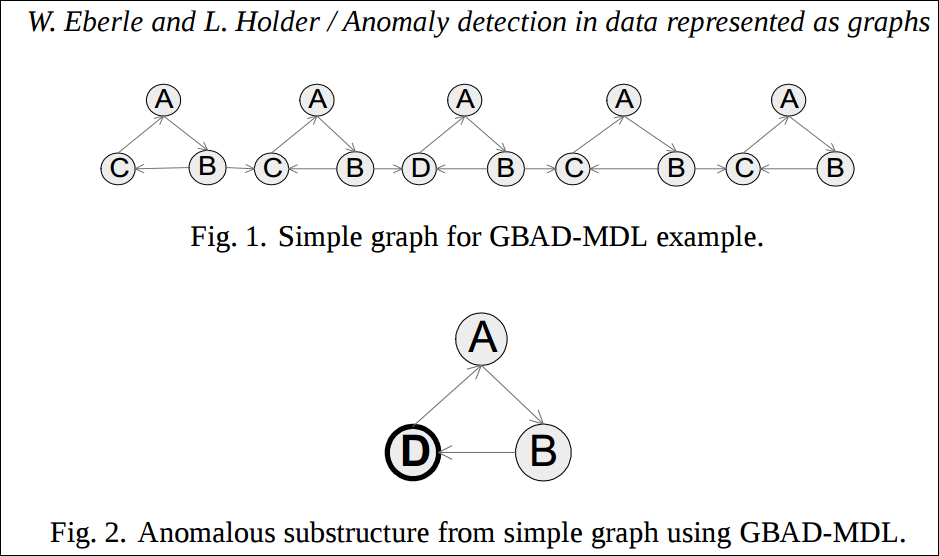
- 그래프에서 최적은 부분구조 S를 찾는데 아래와 같은 그림이 될 것이다.
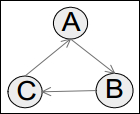
- 모든 I인스턴스를 찾는다. 그건 Fig. 2가 될 것이다.
- Fig. 2는 Frequency도 1이고 변형비용도 vertext하나만 바꾸면 되니 1이다. 즉 최종 출력값은 1 * 1이 될테니 비정상 지수가 1이고 우리가 임계치를 (예를 들어) 3 이하로 잡았다면 해당이 되니까 검출이 될 것이다.
Probabilistic algorithm (GBAD-P)
GBAD-P 알고리즘 또한 MDL 을 사용하여 그래프에서 최적의 부분 구조를 찾아낸다. 다만, S의 모든 인스턴스의 유사성을 비교하는 대신에 이 접근법은 정상 기본구조 패턴의 확장만 검사하여 가장 낮은 확률로 확장될수 있는 패턴을 찾는다. 말이어려운데 S에서 추가로 Insert가 일어나는 패턴중 제일 흔하지 않은 패턴을 찾는다는 것이다. 두 알고리즘의 미묘한 차이는 GBAD-MDL은 같은 특성(size or degree)을 지닌 S의 모든 인스턴스를 찾는 반면에 GBAD-P는 정상 패턴의 확장의 확률을 검사한다. 이를 통해 확률적으로 낮게 일어나는 확장 구조를 찾는다. 추상화된 GBAD-P 알고리즘의 접근법은:
- 그래프 G에서 가장 적합한 정상 패턴인 S(G의 MDL)를 찾는다.
- G에서
- 단일 edge나 vertex의 확장 E를 찾는다. S의 인스턴스 I의 확장에서 가장 낮은 확률 P를 가진 E를 찾는다.
- P가 최소화 되는 I와 E를 출력한다.
- 임계치 이하의 I와 E의 조합을 비정상 패턴으로 출력한다.
- G를 다시 S로 압축하고 여전히 발견되는 부분구조에서의 확장이 있는지 반복하여 찾아본다.
각각의 반복에서 결과값은 S를 포함하고 확장이 가장 낮은 확률값을 가질것이다. 이와 관련된 값은 더 낮은 값을 가질수록 더 비정상 패턴일 가능성이 높다.
예제
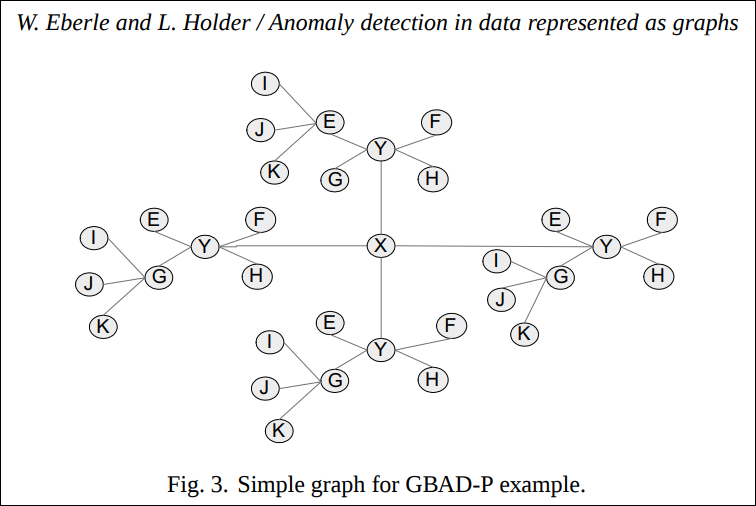
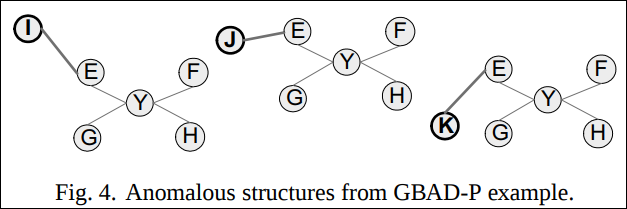
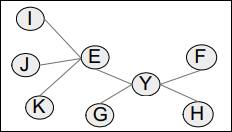
Fig. 3을 전체 그래프라고 보았을 때 그래프의 형태는 X vertex를 기준으로 스타형 구조의 부분 그래프들이 엮여 있다. 각 부분 그래프는 비슷한 패턴의 부분구조이다.(I, J, K를 가지치기 한다는 것까지 포함하여) 하지만 특이한 점은 대부분은 부분 그래프는 G에 I, J, K가 붙어있는데 한곳만 E에 붙어있다.
GBAD-P 알고리즘을 돌리면 Fig. 4와 같은 3가지 구조가 비정상으로 검출된다.
그 이후 부분 반복을 돌려보면 더이상의 비정상이 발견되지 않는다. 부분 후보군에서는 확률이 100%이다. 이유는 최적의 부분구조가 단일 vertex로 압축되니까 I, J, K가 E에 붙어있는지 G에 붙어있는지가 단일 Vertex로 edge가 바뀌기 때문에 모두 다 동일한 구조를 지니는 것으로 인식되기 때문이다.
Maximum partial substructure algorithm (GBAD-MPS)
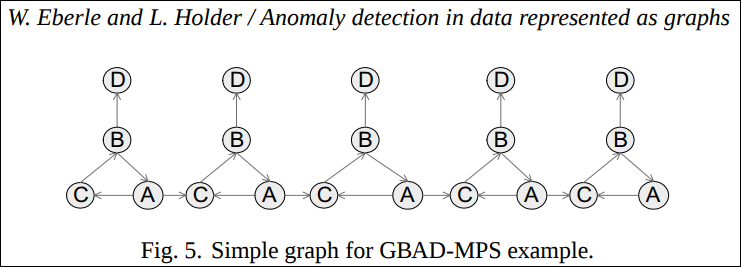
GBAD-MPS 알고리즘은 MDL을 사용하여 최적의 부분 구조 를 찾고 모든 인스턴스에서 비슷한 구조중에 vetex나 edge가 생략된 구조를 찾는다. 추상화된 알고리즘의 접근법은:
- 그래프 G에서 최적의 부분구조 S를 찾는데 S는 G의 MDL이다.
- S의 조상 인스턴스를 찾는다.(조상 부분집합 S’라고 부른다.)
즉 S로 edge 확장되기 전의 인스턴스를 찾는다. - S’의 모든 인스턴스 I중에 S의 인스턴스는 아니지만 S’의 인스턴스를 출력값으로 내보내는데 I는 S의 인스턴스는 아니지만 가장 가까운 변형 비용을 가진다.(변형 비용이 같다면 빈도수가 낮은 것을 택한다.)
예제
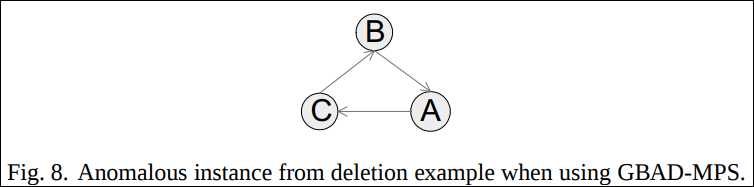
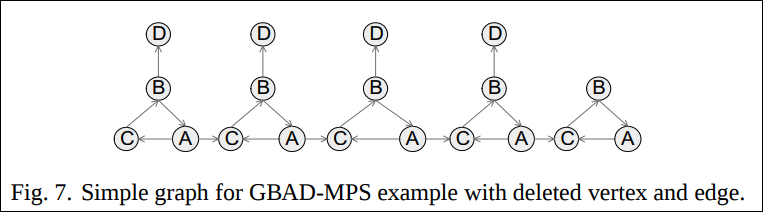
예를 들어 아래의 그래프에서 제일 오른쪽의 D를 하나 지워 그 다음에 나오는 그래프로 만들어버렸다고 가정하자.
위 그래프에서의 best structure는 아래와 같다.
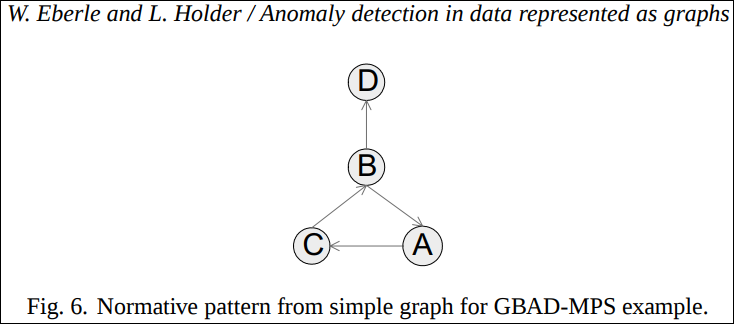
아래의 Fig. 8은 Fig. 6로 확장되기 전인 ancestor structure이다.
Fig. 8 인스턴스는 best structure인 Fig. 6의 인스턴스는 아니고 변형비용 2.0을 가진 ancestor structre의 인스턴스이다. 따라서 비정상 패턴으로 감지된다.
요약하자면 GBAD-MPS를 통해서는 best structure에 최대한 가까운 부분 패턴(Maximum Partial Structure)를 찾을 수 있다.