개요
지난 시간에 이어 Coursera Machine Learning으로 기계학습 배우기 : week3 정리를 진행한다.
목차
해당 포스팅은 연재글로써 지난 연재는 아래의 링크를 참고한다.
글을 읽기에 앞서…
- 본글은 필자가 코세라 기계학습을 공부를 하는 과정에서 개념을 확고히 정리하기 위하는데 목적이 있다. (필자가 나중에 내용을 다시 찾아보기 위한 목적이 있다.)
- 코세라 강의 week 개수에 맞추어 포스팅을 진행할 예정이다.
- 코세라의 슬라이드에 한글 주석을 단것이 핵심으로 내용에서 글을 읽을 필요 없이 슬라이드 그림만으로 최대한 이해가 되게끔 하는데 목적이 있다.
- 수학은 한국의 고등수학을 베이스로 한다. 수학적 개념이 나올때 가급적 고등학교 수학을 베이스로 내용을 정리한다.
- 정리내용의 목차 구성을 코세라 강의와 동일하게 맞추고 또한 제목을 원문으로 둔다. (원본강의 내용과 정리 내용을 서로 서로 찾아보기 쉽게하기 위함이다.)
====================== 3강 ============================================
Classification and Representation
Classification
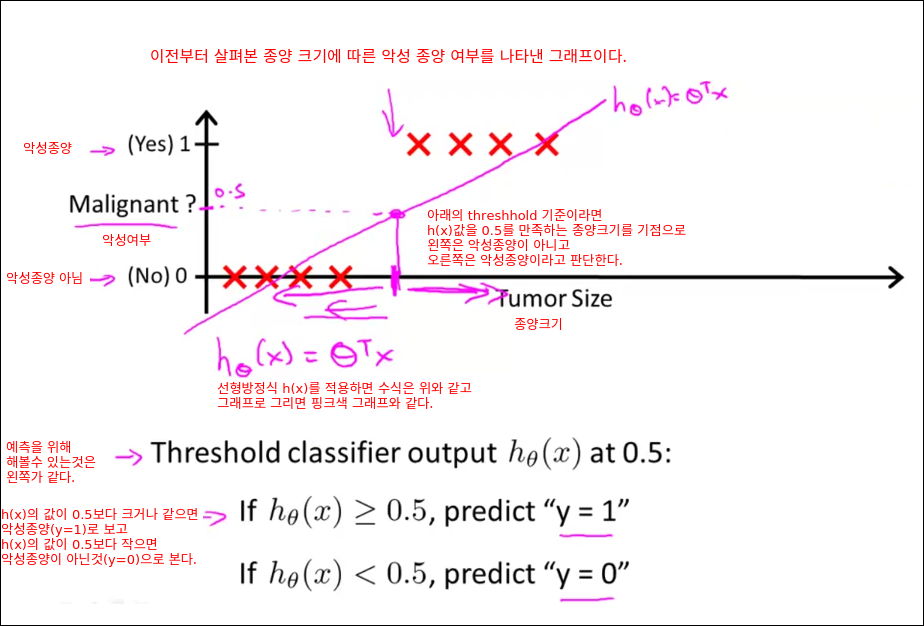
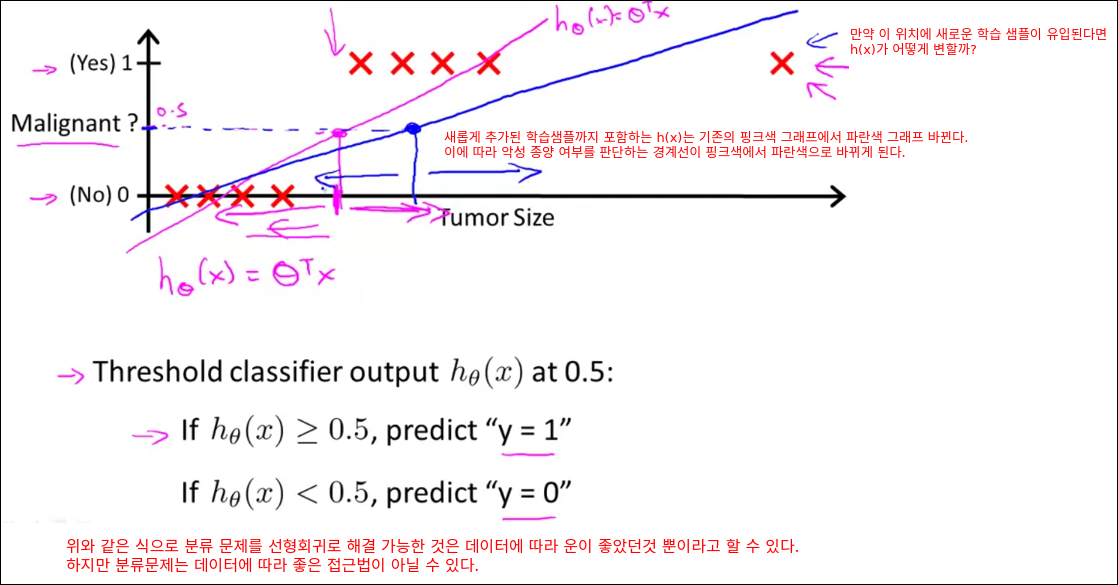
보통 분류하기를 원하는 결과를 Positive로 두는 경향이 있다.



Hypothesis Representation


로지스틱 함수(g함수) 중에 하나가 sigmoid 함수이다.
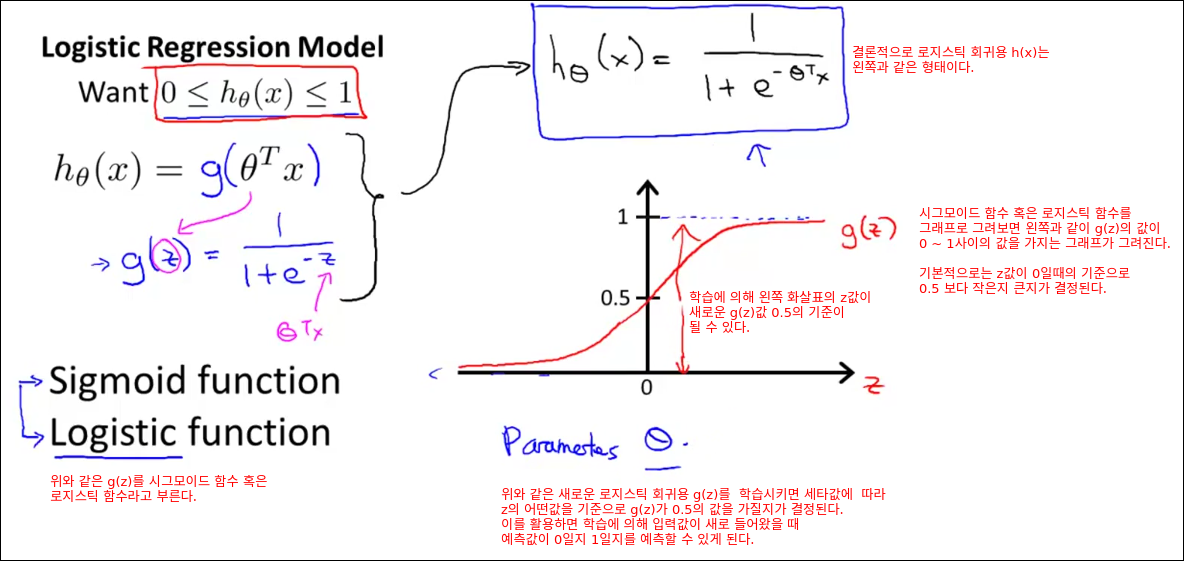
로지스틱 회귀의 장점 중 하나는 출력값의 확률(가능성)을 가늠할 수 있다는 것이다.

Decision Boundary

사실 선형의 결정경계를 구하는 경우의 수는 무한대에 가깝다.
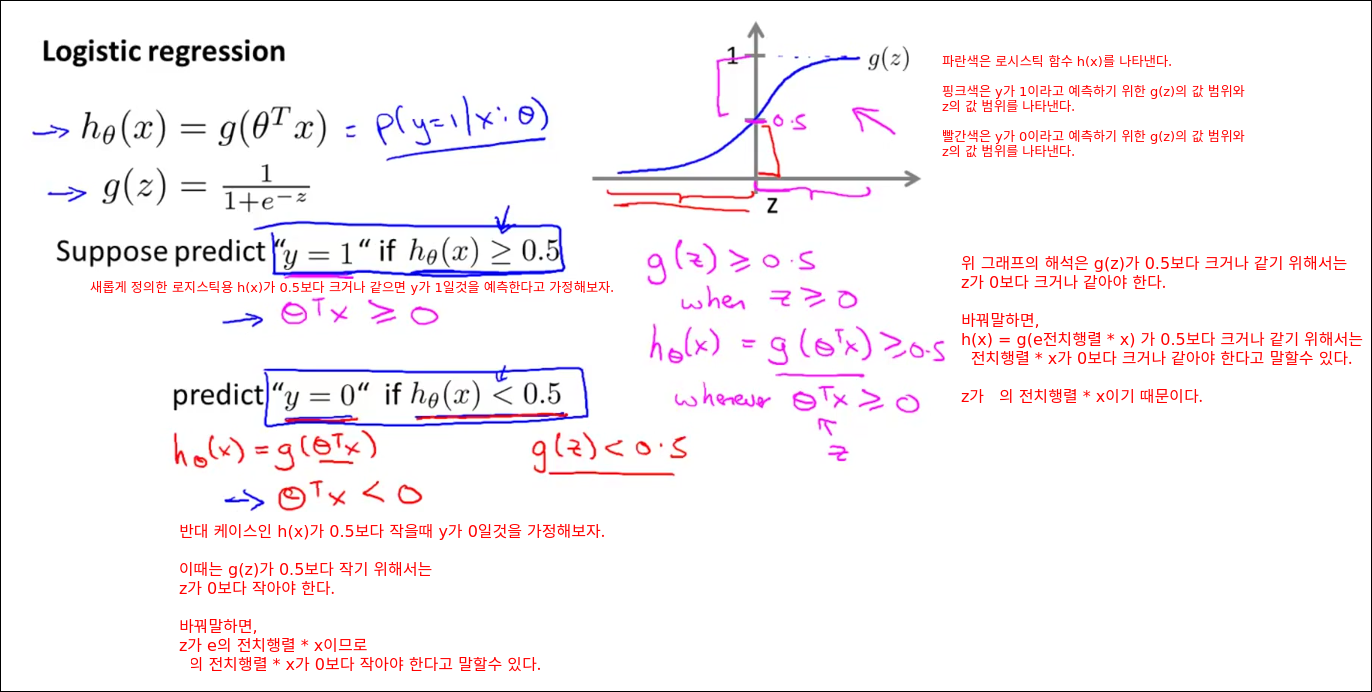






Logistic Regression Model
Cost Function




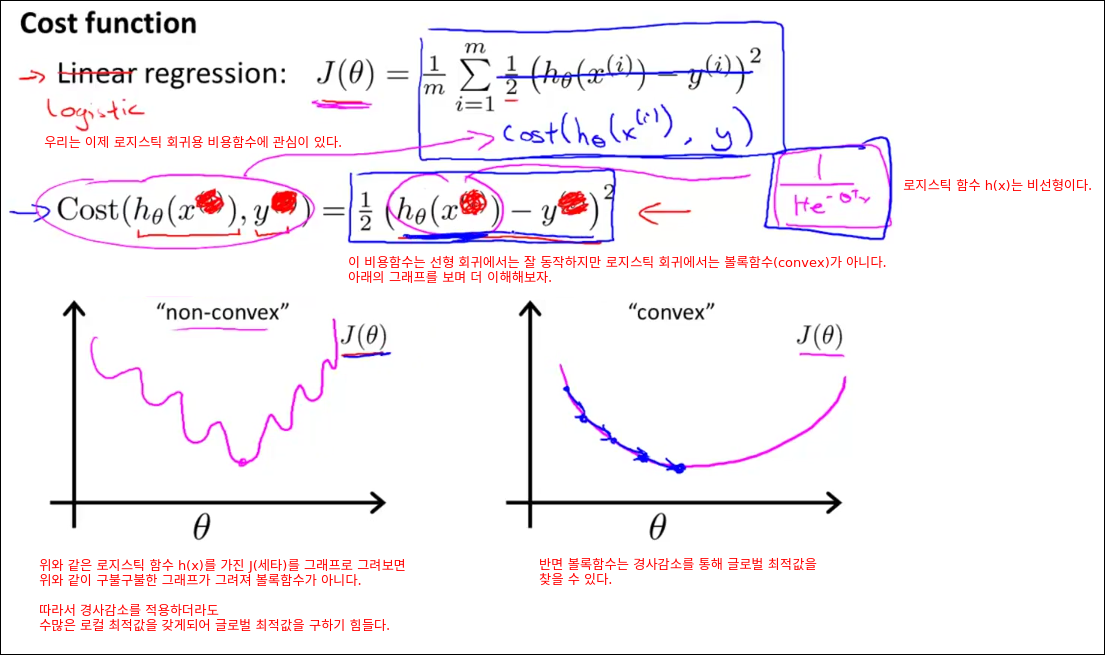

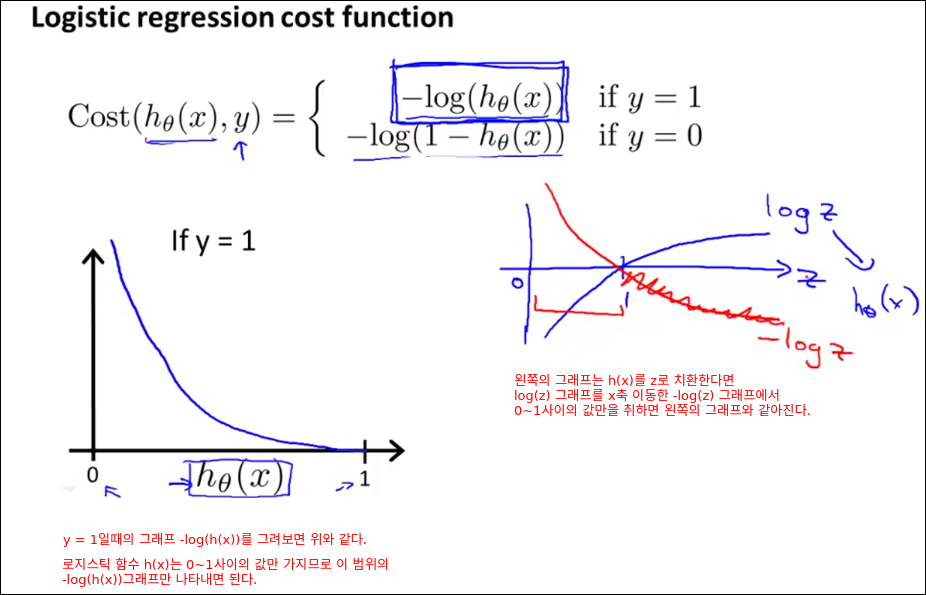

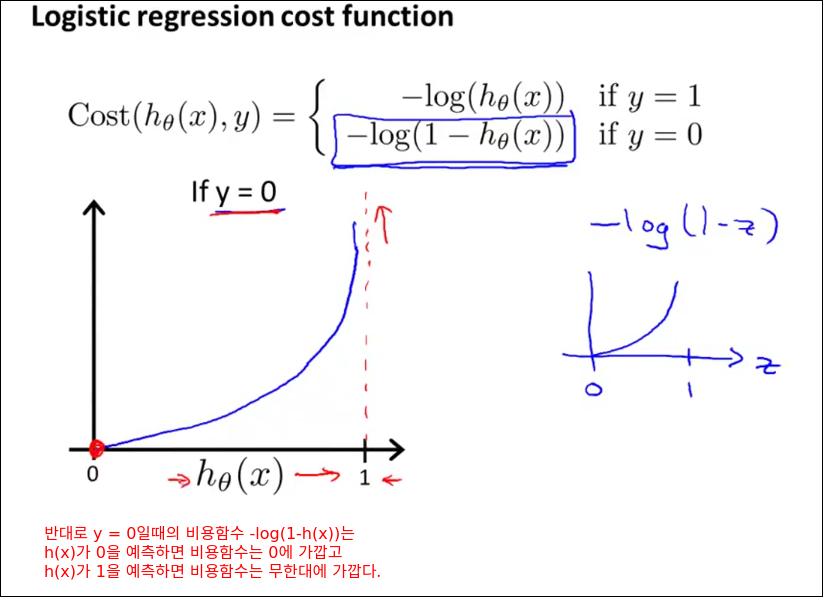
Simplified Cost Function and Gradient Descent




선형 회귀의 경사감소법과 로지스틱 회귀의 경사감소법 수식은 완전히 똑같다. 다만 h(x) 정의가 다르다. 그리고 수식의 의미는 가설함수의 값과 정답지의 값의 차이를 입력값의 크기에 비례해서 세타값을 줄이라는 의미이다.


Advanced Optimization





이부분을 옥타브를 이용하여 직접 실숩하여 보자.
아래와 같이 costFunction 함수를 만든다.
costFunction.m
function [jVal, gradient] = costFunction(theta)
jVal = (theta(1) - 5) ^ 2 + (theta(2) - 5) ^ 2
gradient = zeros(2, 1);
gradient(1) = 2 * (theta(1) - 5);
gradient(2) = 2 * (theta(2) - 5);
이제 옥타브 커맨드라인에서 costFunction.m이 있는 경로에서 아래의 3줄의 명령어를 입력해본다.
>> options = optimset('GradObj', 'on', 'MaxIter', '100');
>> initTheta = zeros(2, 1);
>> [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initTheta, options);
그러면 알파값을 지정하지 않았음에도 fminunc()에 의해 비용함수가 최소화 된것을 확인 할 수 있다.
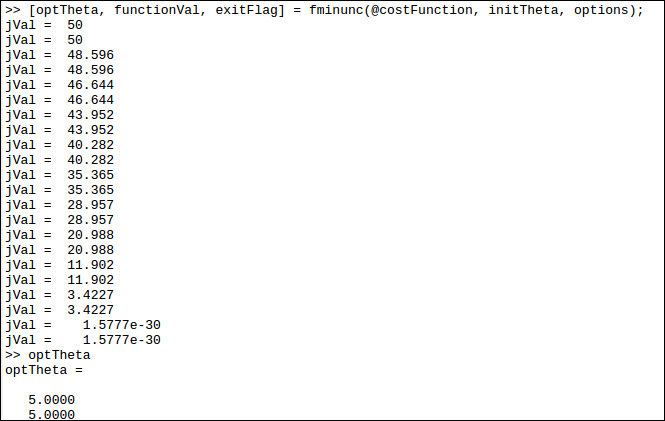
또한 쎄타값을 확인해보면 세타값이 기존의 0에서 바뀐것을 확인 할 수 있다.

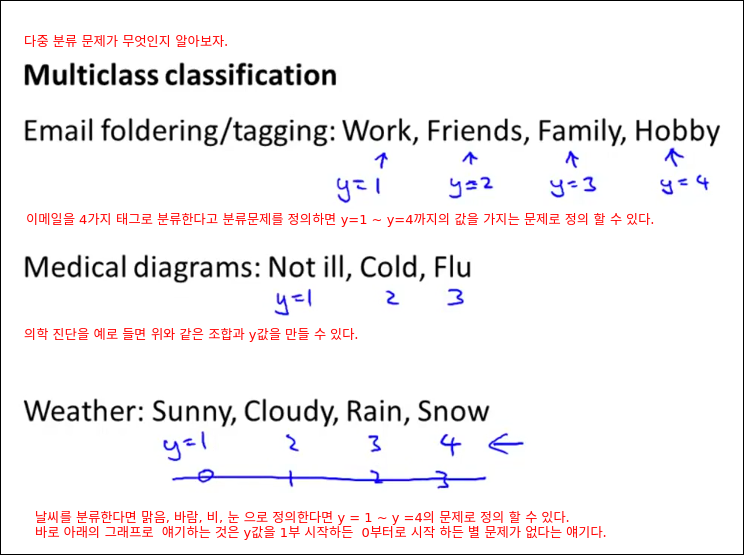
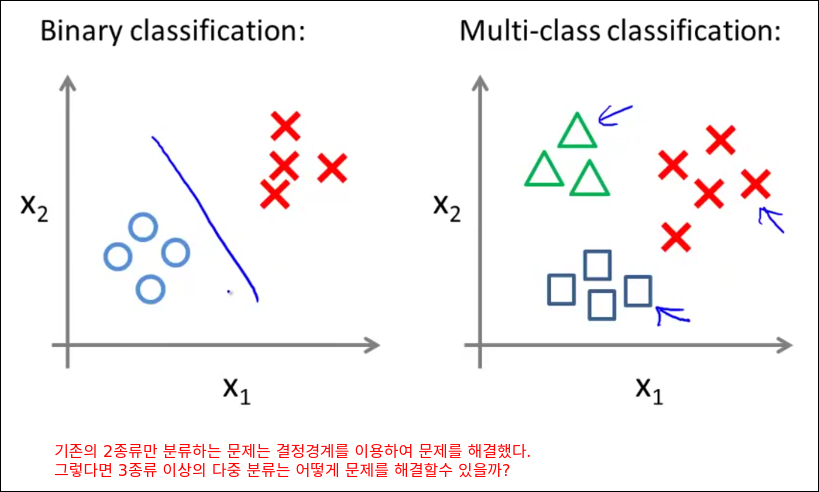
Multiclass Classification

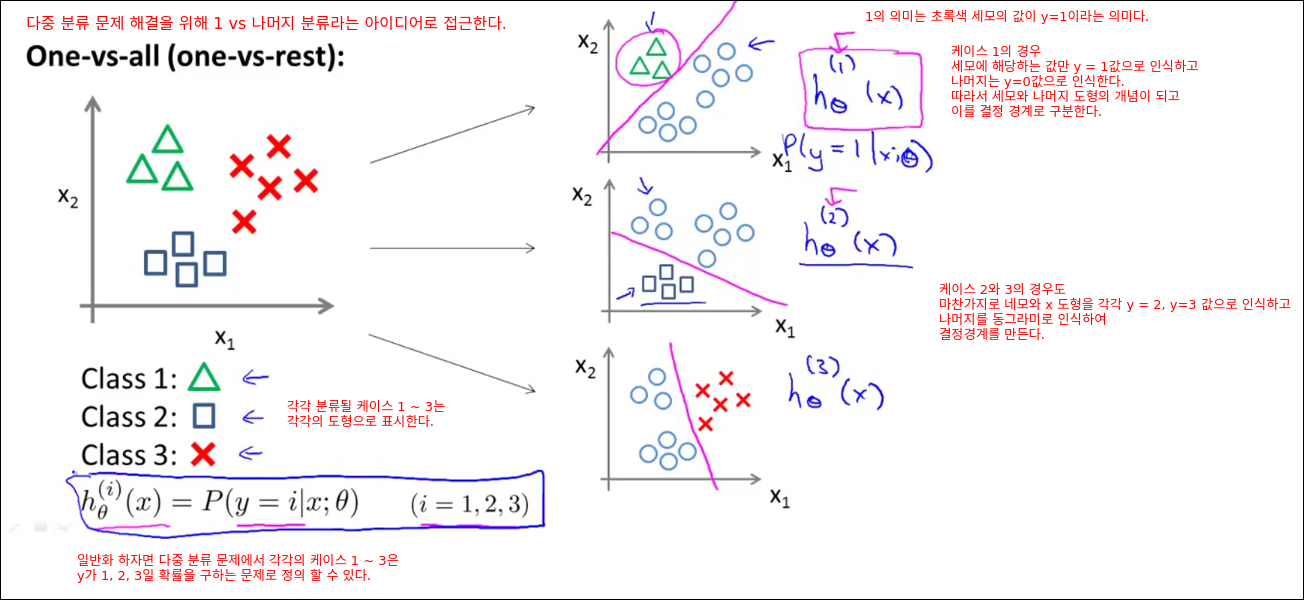

Solving Problem of Overfitting
The Problem of Solving Overfitting

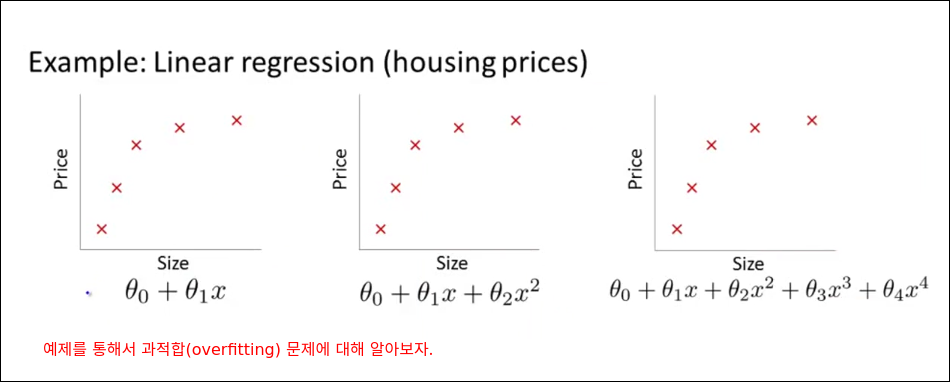
bias와 variance의 딜레마다.
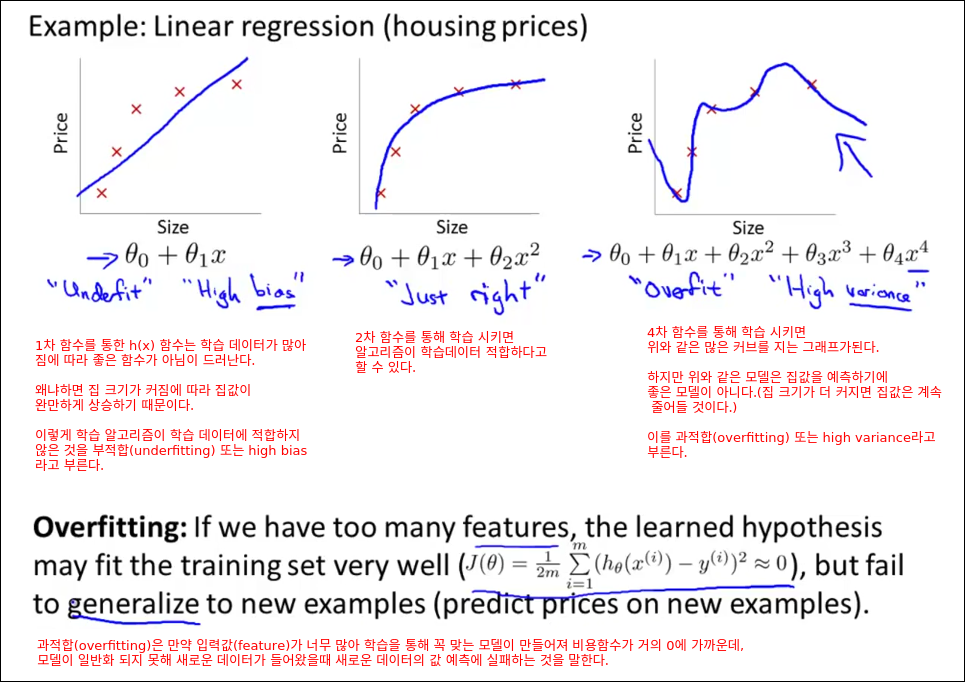
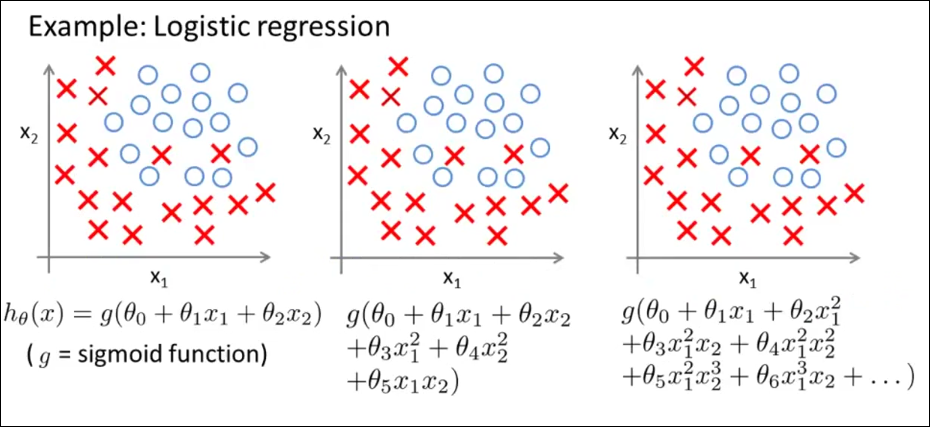
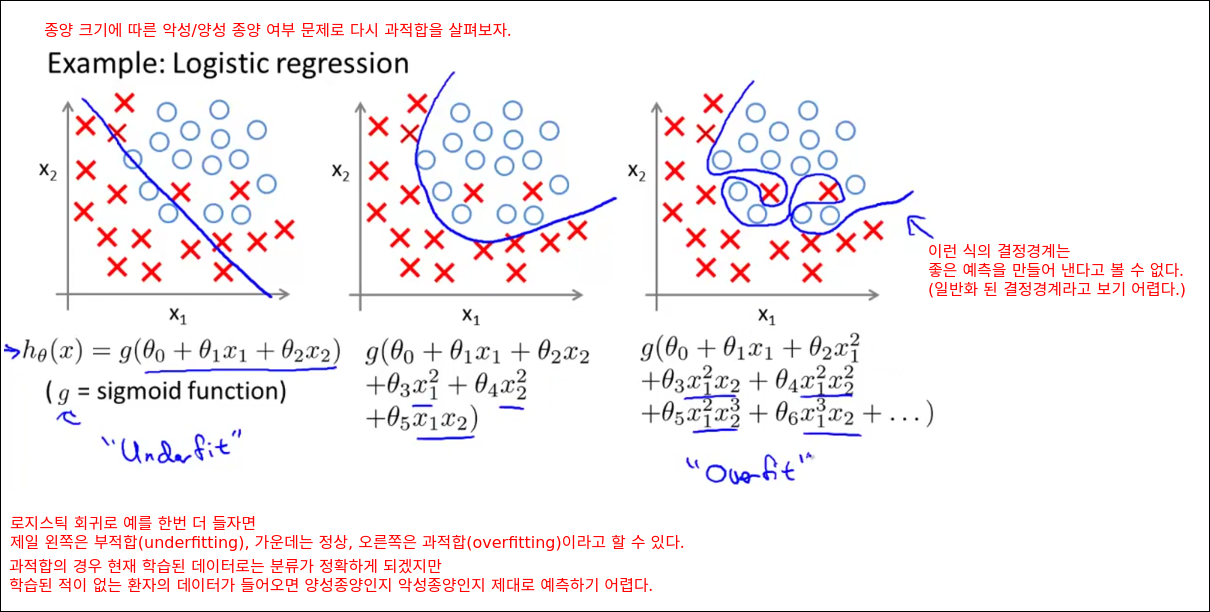


Cost Function

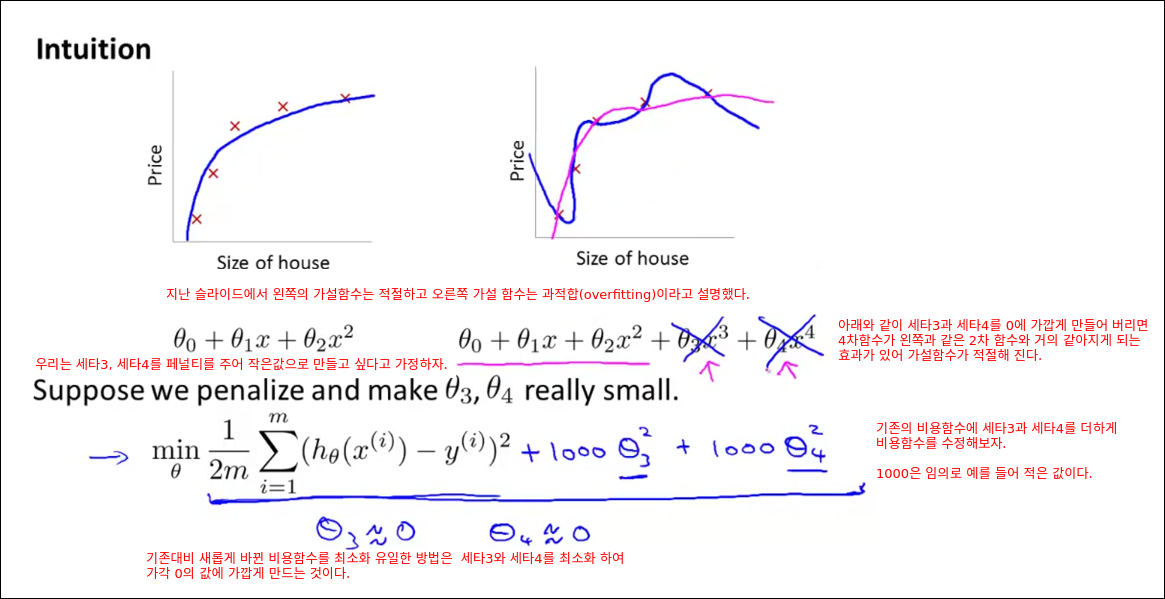

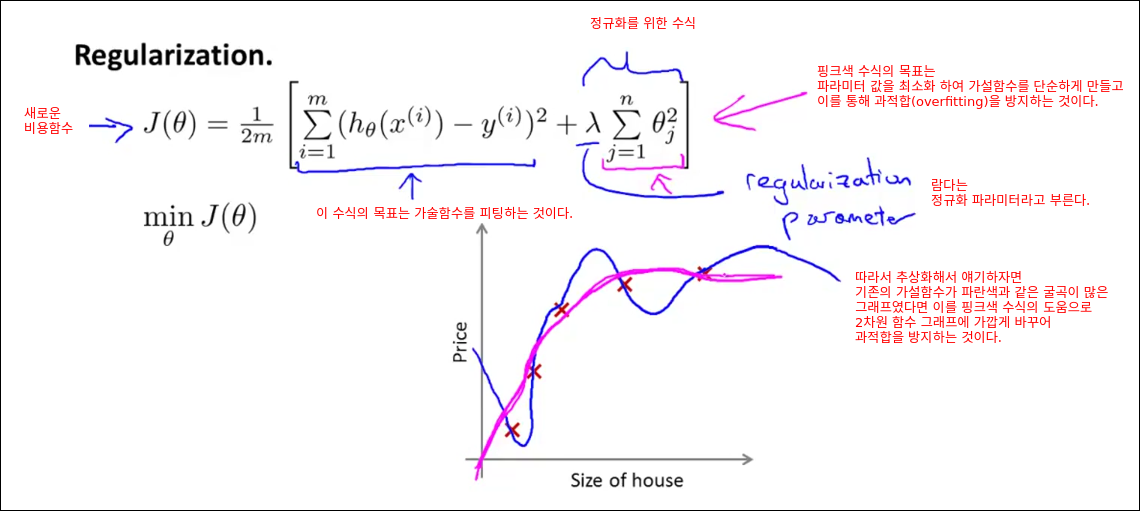

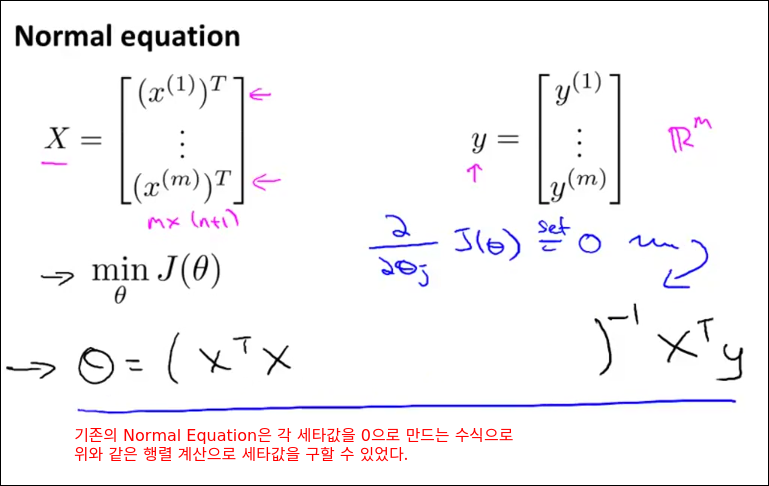
Regular Linear Regression





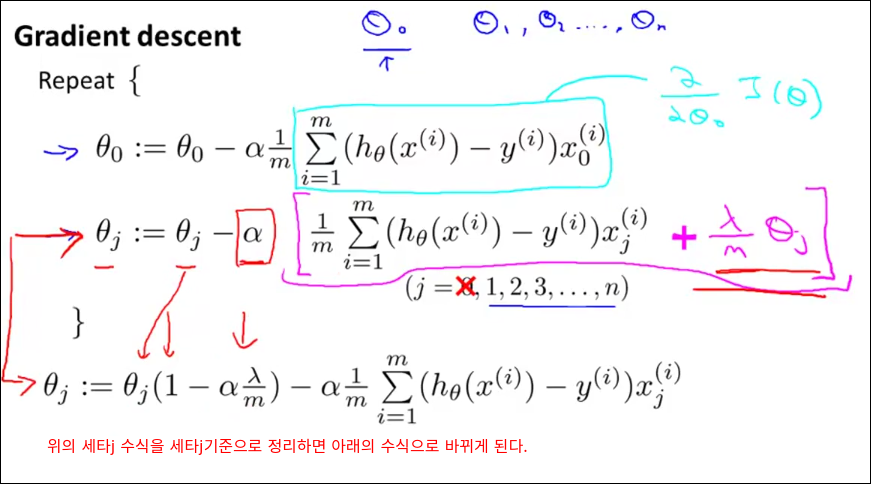


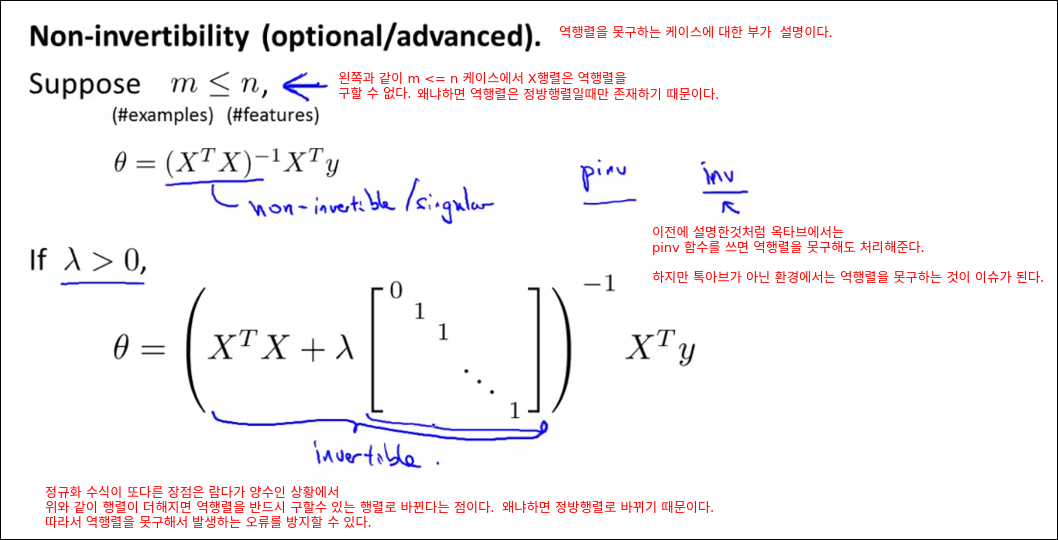
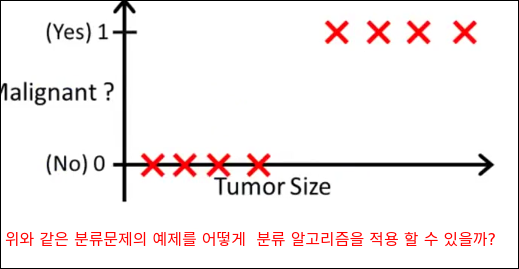
Regularized Logistic Regression